题目内容
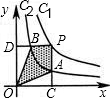 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、k1+k2 | ||
| B、k1-k2 | ||
| C、k1•k2 | ||
D、
|
分析:四边形PAOB的面积为矩形OCPD的面积减去三角形ODB与三角形OAC的面积,根据反比例函数y=
中k的几何意义,其面积为k1-k2.
| k |
| x |
解答:解:根据题意可得四边形PAOB的面积=S矩形OCPD-SOBD-SOAC,
由反比例函数y=
中k的几何意义,可知其面积为k1-k2.
故选B.
由反比例函数y=
| k |
| x |
故选B.
点评:主要考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
| k |
| x |

练习册系列答案
相关题目
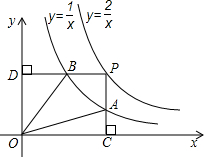 如图,两个反比例函数y=
如图,两个反比例函数y=| 2 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
| 1 |
| x |
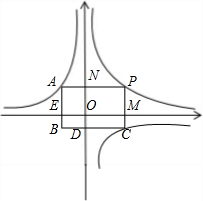 如图,两个反比例函数y=
如图,两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| A、|k1-k2| | ||
B、
| ||
| C、|k1•k2| | ||
D、
|
 (2012•德州)如图,两个反比例函数
(2012•德州)如图,两个反比例函数 如图,两个反比例函数y=
如图,两个反比例函数y=