Question

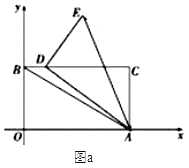
【题目】如图，平行四边形ABCD中，点P为CB延长线上点，连接DP交AC于点M、交AB于点N，已知DA＝DC，∠ACD＝45°．

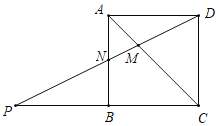
（1）求证：四边形ABCD为正方形；

（2）连接BM，若N为AB的中点，求tan∠BMP的值；

（3）若MN＝2，PN＝6，求DM的长．

Answer 1

【答案】（1）见解析；（2）；（3）4

【解析】

（1）有1个角为90°的菱形为正方形.

（2）证明△BPN≌△AND，然后用相似三角形性质求解

（3）MD2＝MNMP

（1）证明：∵四边形ABCD是平行四边形，DA＝DC，

∴四边形ABCD是菱形，

∵DA＝DC，

∴∠ACD＝∠CAD＝45°，

∴∠ADC＝90°，

∴四边形ABCD为正方形；

（2）解：作BE⊥PD，如图所示：

则∠PEB＝∠MEB＝90°，

设正方形ABCD的边长为a，

∵四边形ABCD是正方形，

∴AD∥BC，AB∥CD，AB＝AD＝a，∠PBN＝∠DAB＝∠BCD＝90°，

∵N为AB的中点，

∴AN＝BN＝AB＝a，

在△BPN和△ADN中，，

∴△BPN≌△ADN（ASA），

∴BP＝AD＝a，PN＝DN＝＝＝a，PC＝BP+BC＝2a，

∴PD＝2DN＝a，

∵AD∥BC，

∴△ADM∽△CPM，

∴，

∴，

∵∠PEB＝∠PCD＝90°，∠P＝∠P，

∴△PBE∽△PDC，

∴，即，

解得：，

∴

∴

（3）解：MN＝2，PN＝6，

∴MP＝8，

∵AB∥CD，

∴AM：MC＝MN：MD，

∵AD∥BC，

∴AM：MC＝DM：MP，

∴MN：MD＝DM：MP，

∴MD2＝MNMP＝2×8＝16，

∴MD＝4．