题目内容
【题目】已知点![]() ,点D在双曲线
,点D在双曲线![]() 的图象上,而点P是直线
的图象上,而点P是直线![]() 上的动点,若这三点与平面上任意一点构成正方形,则点D的坐标为____________.
上的动点,若这三点与平面上任意一点构成正方形,则点D的坐标为____________.
【答案】(3,4)或(4,3)或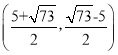 或
或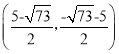 或(-12,-1)
或(-12,-1)
【解析】
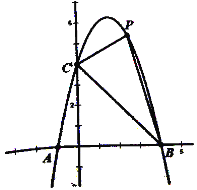
由题意,只要ADP组成等腰直角三角形就可以,讨论分别以A、D、P为直角顶点的直角三角形,可得出结论.
由题意,只要△ADP为等腰直角三角形就可以构成正方形,
①如图所示,若∠ADP=90°,AD=DP,过D作EF∥x轴,则可得DE⊥AE,DF⊥PF,
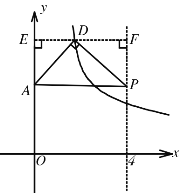
∵∠ADP=90°,∴∠ADE+∠PDF=90°,
又∵∠EAD+∠ADE=90°,∴∠EAD=∠PDF,
在△ADE和△DPF中,

∴△ADE≌△DPF(AAS)
∴DE=PF,AE=DF,
设D点坐标![]() ,P点坐标为
,P点坐标为![]() ,则DE=PF=m,AE=DF=4-m
,则DE=PF=m,AE=DF=4-m
∵A点纵坐标为3,∴OA=3,E点纵坐标为3+4-m=7-m,与D点纵坐标相等,
则![]() ,解得m=3或4,则D点坐标为(3,4)或(4,3);
,解得m=3或4,则D点坐标为(3,4)或(4,3);
②如图所示,若∠APD=90°,AP=DP,过P作EF∥x轴,过D作DF∥y轴,则可得PE⊥AE,DF⊥PF,
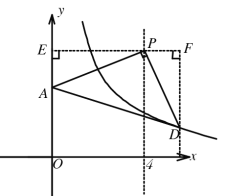
同①可证△PAE≌△DPF,∴PE=DF,AE=PF,
设D点坐标![]() ,P点坐标为
,P点坐标为![]() ,则PE=DF=4,AE=PF=m-4,
,则PE=DF=4,AE=PF=m-4,
由E点和F点纵坐标相同可得,![]() ,解得,
,解得,![]() ,所以D点坐标为
,所以D点坐标为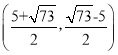 或
或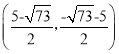
③如图所示,若∠PAD=90°,AD=AP,过A作EF∥x轴,过D点作DE∥y轴,则可得AE⊥DE,AF⊥PF,
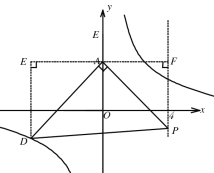
同理可证△ADE≌△PAF,所以AE=PF,DE=AF,
设D点坐标![]() ,P点坐标为
,P点坐标为![]() ,则AE=PF=-m,DE=AF=4,
,则AE=PF=-m,DE=AF=4,
由E点纵坐标与A点纵坐标相等,可得![]() ,解得m=-12,
,解得m=-12,
所以D坐标为(-12,-1)
综上所述D点坐标为(3,4)或(4,3)或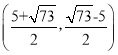 或
或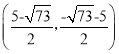 或(-12,-1)
或(-12,-1)

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
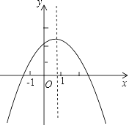
黄冈海淀全程培优测试卷系列答案【题目】在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )
A. m>n B. m<n C. m=n D. 无法确定