题目内容
【题目】如图1,抛物线 y=ax2+bx+c 与 x 轴交于A(1,0),B(-3,0),与 y 轴交于C(0,3),顶点是G.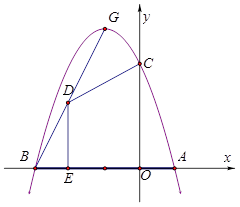
(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线 y=ax2+bx+c 向下平移 k 个单位,平移后的顶点式 G' ,与 x 轴的交点是 A',B' .若△A'B'G' 是直角三角形,求 k 的值.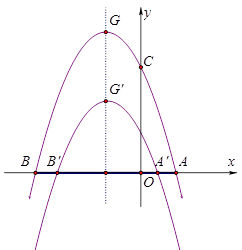
【答案】
(1)解:∵与 x 轴的交点为A(1,0),B(-3,0),
∴设二次函数为 y=a(x+1)(x3),
把C(0,3)代入 y=a(x+1)(x3),
∴ a=-1 ,
∴ y=-x2-2x+3=-(x+1)2+4.
∴G(-1,4).
(2)解:设直线BG解析式为 :y=kx+b
∵B(3,0),G(1,4) 在直线BG上,
∴![]() ,
,
∴![]() ,
,
∴ 直线BG解析式为:y=2x+6,
∴ D(x,2x+6)
∴ S=![]() =
=![]() =-x2-
=-x2-![]() x ( 3<x<1 ),
x ( 3<x<1 ),
当 x=-![]() =-
=-![]() 时,Smax=
时,Smax=![]() .
.
(3)解:设平移后的抛物线为 y=(x+1)2+m,
∴G'(-1,m),A'(-1-![]() ,0),B'(-1+
,0),B'(-1+![]() ,0),
,0),
∴A'B'=2![]() ,B'G'=A'G'=
,B'G'=A'G'=![]() ,
,
∵△A'B'G'为直角三角形,
∴B'G'2+A'G'2=A'B'2,
∴m2m=0,
∴ m1=1 , m2=0 (舍),
∴ y=(x+1)2+1,
∵由 y=(x+1)2+4 得到 y=(x+1)2+1
∴ 向下平移3个单位,
∴ k=3.
【解析】(1)根据题意可设二次函数为 y=a(x+1)(x3),将C(0,3)代入 y=a(x+1)(x3),从而求出抛物线解析式,即可得出顶点坐标.
(2)设直线BG解析式为 :y=kx+b把B(3,0),G(1,4) 代入即可得到一个二元一次方程组,解之即可得出直线BG解析式为:y=2x+6,从而表示D(x,2x+6),再由S=![]() =
=![]() =-x2-
=-x2-![]() x ( 3<x<1 ),由二次函数的性质得出当 x=-
x ( 3<x<1 ),由二次函数的性质得出当 x=-![]() =-
=-![]() 时,Smax=
时,Smax=![]() .
.
(3)设平移后的抛物线为 y=(x+1)2+m,根据题意得G'(-1,m),A'(-1-![]() ,0),B'(-1+
,0),B'(-1+![]() ,0),A'B'=2
,0),A'B'=2![]() ,B'G'=A'G'=
,B'G'=A'G'=![]() ,
,
在Rt△A'B'G'中,由勾股定理得m2m=0,从而求出m值,即可得出k值.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握二次函数图象的平移(平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减)的相关知识才是答题的关键.

【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.