ЬтФПФкШн
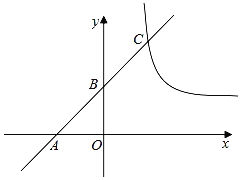
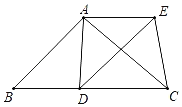
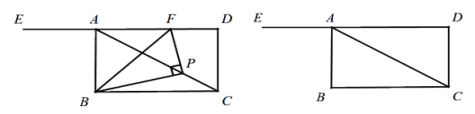
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧОиаЮЃЌЕуPЪЧЖдНЧЯпACЩЯвЛЖЏЕуЃЈВЛгыЕуCКЭЕу![]() жиКЯЃЉЃЌСЌНгPBЃЌЙ§ЕуPзї
жиКЯЃЉЃЌСЌНгPBЃЌЙ§ЕуPзї![]() НЛЩфЯпDAгкЕуFЃЌСЌНгBFЃЎ вбжЊAD=3
НЛЩфЯпDAгкЕуFЃЌСЌНгBFЃЎ вбжЊAD=3![]() ЃЌCD=3ЃЌЩшCPЕФГЄЮЊxЃЌ
ЃЌCD=3ЃЌЩшCPЕФГЄЮЊxЃЌ
ЃЈ1ЃЉЯпЖЮ![]() ЕФзюаЁжЕ ЃЌЕБx=1ЪБЃЌ
ЕФзюаЁжЕ ЃЌЕБx=1ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃЌЕБЖЏЕу![]() дЫЖЏЕНACЕФжаЕуЪБЃЌ
дЫЖЏЕНACЕФжаЕуЪБЃЌ![]() гы
гы![]() ЕФНЛЕуЮЊGЃЌ
ЕФНЛЕуЮЊGЃЌ![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌЧѓЯпЖЮGHЕФГЄЖШЃЛ
ЃЌЧѓЯпЖЮGHЕФГЄЖШЃЛ
ЃЈ3ЃЉЕБЕу![]() дкдЫЖЏЕФЙ§ГЬжаЃЌ
дкдЫЖЏЕФЙ§ГЬжаЃЌ
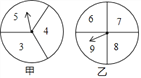
ЂйЪдЬНОП![]() ЪЧЗёЛсЗЂЩњБфЛЏЃПШєВЛИФБфЃЌЧыЧѓГі
ЪЧЗёЛсЗЂЩњБфЛЏЃПШєВЛИФБфЃЌЧыЧѓГі![]() ДѓаЁЃЛШєИФБфЃЌЧыЫЕУїРэгЩЃЛ
ДѓаЁЃЛШєИФБфЃЌЧыЫЕУїРэгЩЃЛ
ЂкЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЪЧЕШбќШ§НЧаЮЃП
ЪЧЕШбќШ§НЧаЮЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ30ЁуЃЛЃЈ2ЃЉ
ЃЌ30ЁуЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂй30ЁуЃЛЂкx=3Лђ3
ЃЛЃЈ3ЃЉЂй30ЁуЃЛЂкx=3Лђ3![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЕБBPзюаЁЪБЃЌМДBPЁЭACЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЃЌПЩЧѓГіBPжЕЃЌЕБx=1ЪБЃЌПЩЕУГіЁїBPNЁзЁїPMFЃЌгЩДЫПЩЕУГіtanЁЯFBPЕФжЕЃЌдђПЩЕУЕНЁЯFBPЕФжЕЃЛ
ЃЈ2ЃЉПЩжЄBPДЙжБЦНЗжAPЃЌЧѓЕУFP=![]() ЃЌжЄGHЪЧRtЁїFGPжаЯпЃЌдђGH=
ЃЌжЄGHЪЧRtЁїFGPжаЯпЃЌдђGH=![]() FPЃЛ
FPЃЛ
ЃЈ3ЃЉЂйЙ§PзїPNЁЭBCНЛADгкMЃЌПЩжЄЁїFMPЁзЁїPNBЃЌЩшPC=xЃЌPN=![]() ЃЌПЩЧѓЕУNCЃЌMPЃЌBNГЄЖШЃЌtanЁЯFBP=
ЃЌПЩЧѓЕУNCЃЌMPЃЌBNГЄЖШЃЌtanЁЯFBP=![]() =
=![]() =
=![]() ЃЌМДПЩЧѓЕУЁЯFBPЕФДѓаЁЃЛ
ЃЌМДПЩЧѓЕУЁЯFBPЕФДѓаЁЃЛ
ЂкЗжШ§жжЧщПіЬжТлЧѓНтМДПЩ.
ЃЈ1ЃЉЕБBPзюаЁЪБЃЌAгыFжиКЯЃЌМДBPЁЭACЃЌ
ЁпAD=3![]() ЃЌCD=3ЃЌ
ЃЌCD=3ЃЌ
ЁрAC=6ЃЌЁЯBAC=30ЁуЃЌ
дкRtЁїABCКЭRtЁїAPBжаЃЌЁЯBAC=ЁЯPABЃЌ
ЁрЁїABCЁзЁїAPBЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрBP=![]() ЃЛ
ЃЛ
зїPMЁЭBCгкNЃЌНЛADгкMЃЌ

ЕБx=1ЪБЃЌPN=![]() ЃЌMP=
ЃЌMP=![]() ЃЌCN=
ЃЌCN=![]() ЃЌBN=
ЃЌBN=![]() ЃЌ
ЃЌ
ЁпЁЯBNP=ЁЯPMF=ЁЯBPM=90ЁуЃЌ
ЁрЁЯFPM+ЁЯPFM=90ЁуЃЌЁЯFPM+ЁЯBPN=90Ёу,
ЁрЁЯPFM=ЁЯBPNЃЌ
ЁрЁїBPNЁзЁїPMFЃЌ
Ёр![]() =
=![]() =
=![]() =tanЁЯFBP=
=tanЁЯFBP=![]() ЃЌ
ЃЌ
ЁрЕБx=1ЪБЃЌЁЯFBP=30Ёу;
ЃЈ2ЃЉЁпPЮЊACжаЕуЃЌ

ЁрAP=PC=AB=3ЃЌ
ЁрЁЯABP=ЁЯAPB=ЁЯBAP=60ЁуЃЌ
дкRtЁїABFКЭRtЁїPBFжаЃЌAB=BPЃЌBF=BFЃЌ
ЁрRtЁїABFЁеRtЁїPBFЃЌ
ЁрAG=PGЃЌЁЯAGB=ЁЯPGB=90ЁуЃЌ
ЁрBFДЙжБЦНЗжAPЃЌ
дкRtЁїBFPжаЃЌЁЯPBF=30ЁуЃЌBP=3ЃЌ
ЁрPF=tan30ЁуЁС3=![]() ЃЌ
ЃЌ
ЁпHЮЊPFжаЕуЃЌ
ЁрGHЮЊRtЁїPGFЕФжаЯпЃЌ
ЁрGH=![]() PF=
PF=![]() ;
;
ЃЈ3ЃЉЂйЁЯFBP=30ЁуЃЌ
Й§PзїPNЁЭBCНЛADгкMЃЌ
ЁпЁЯPBN=ЁЯFPMЃЌЁЯBPN=ЁЯPFMЃЌ
ЁрЁїFMPЁзЁїPNBЃЌ
ЩшCP=xЃЌдђPN=![]() ЃЌNC=
ЃЌNC=![]() xЃЌMP=3-
xЃЌMP=3-![]() xЃЌBN=3
xЃЌBN=3![]() -
-![]() xЃЌ
xЃЌ
ЁрtanЁЯFBP=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁрЁЯFBP=30ЁуЃЛ
ЂкЃЈiЃЉШєAF=FPЃЌдђЁЯFPA=ЁЯFAP=30ЁуЃЌ
ЁрAB=BPЃЌЧвЁїABPЮЊЕШБпШ§НЧаЮЃЌ
ЁрBFЮЊЁїABPДЙжБЦНЗжЯпЃЌ
ЁрAB=BP=3ЃЌМДx=3ЃЛ
ЃЈiiЃЉШєAP=FPЃЌдђЁЯAPF=120ЁуЃО90ЁуЃЈЩсШЅЃЉЃЛ
ЃЈiiiЃЉШєAP=AFЃЌдђЁЯCBP=ЁЯCPB=75ЁуЃЌBC=PCЃЌДЫЪБx=3![]() .
.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ