Question

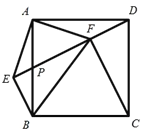
【题目】如图,点是正方形边上一点,连接,作于点,手点,连接．

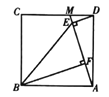
(1)求证:；

(2已知,四边形的面积为24,求的正弦值．

Answer 1

【答案】(1)证明见解析；(2) ．

【解析】（1）通过证明△ABF≌△DEA得到BF=AE；

（2）设AE=x，则BF=x，DE=AF=2，利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到xx+x2=24，解方程求出x得到AE=BF=6，则EF=x-2=4，然后利用勾股定理计算出BE，最后利用正弦的定义求解．

详（1）证明：∵四边形ABCD为正方形，

∴BA=AD，∠BAD=90°，

∵DE⊥AM于点E，BF⊥AM于点F，

∴∠AFB=90°，∠DEA=90°，

∵∠ABF+∠BAF=90°，∠EAD+∠BAF=90°，

∴∠ABF=∠EAD，

在△ABF和△DEA中

，

∴△ABF≌△DEA（AAS），

∴BF=AE；

（2）解：设AE=x，则BF=x，DE=AF=2，

∵四边形ABED的面积为24，

∴xx+x2=24，解得x1=6，x2=-8（舍去），

∴EF=x-2=4，

在Rt△BEF中，BE=，

∴sin∠EBF=．