题目内容
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)在y轴上找出一点P,使得PA+PB的值最小,直接写出点P的坐标;
(3)在平面直角坐标系中,找出一点A2 , 使△A2BC与△ABC关于直线BC对称,直接写出点A2的坐标.
【答案】
(1)
解:如图所示;
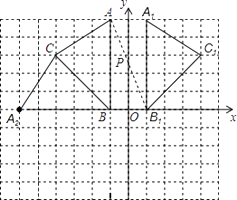
(2)
解:设直线AB1的解析式为y=kx+b(k≠0),
∵A(﹣1,5),B1(1,0),
∴ ![]() ,解得
,解得 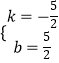 ,
,
∴直线AB1的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
∴P(0,2.5);
(3)
解:如图所示,A2(﹣6,0).
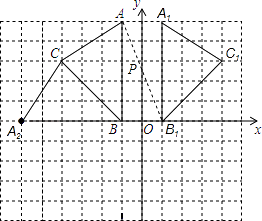
【解析】(1)先作出各点关于y轴的对称点,再顺次连接即可;(2)连接AB1交y轴于点P,利用待定系数法求出直线AB1的解析式,进而可得出P点坐标;(3)找出点A关于直线BC的对称点,并写出其坐标即可.
【考点精析】本题主要考查了确定一次函数的表达式和坐标与图形变化-对称的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)才能正确解答此题.

【题目】光明中学七(1)班40个同学每10人一组,每人做10次抛掷两枚硬币的实验,想想看“出现两个正面”的频率是否会逐渐稳定下来,得到了下面40个实验结果。
第一组学生学号 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
两个正面成功次数 | 1 | 2 | 3 | 3 | 3 | 3 | 3 | 6 | 3 | 3 |
第二组学生学号 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
两个正面成功次数 | 1 | 1 | 3 | 2 | 3 | 4 | 2 | 3 | 3 | 3 |
第三组学生学号 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
两个正面成功次数 | 1 | 0 | 3 | 1 | 3 | 3 | 3 | 2 | 2 | 2 |
第四组学生学号 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 |
两个正面成功次数 | 2 | 2 | 1 | 4 | 2 | 4 | 3 | 2 | 3 | 3 |
(1)学号为113的同学在他10次实验中,成功了几次?成功率是多少?他是他所在小组同学中成功率最高的人吗?
(2)学号为116和136的两位同学在10次实验中成功率一样吗?如果他们两人再做10次实验,成功率依然会一样吗?
(3)怎么计算每一组学生的集体成功率?哪一组成功率最高?
(4)累计每个学生的实验结果,完成下面的“出现两个正面”的频数、频率随抛掷次数变化统计表,如果把这张表画成相应的图,你会看到什么?
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
出现两个正面的频数 | ||||||||
出现两个正面的频率 |