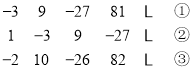题目内容
【题目】如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,求AB和CD间的距离.
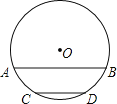
【答案】解:分别作弦AB、CD的弦心距,设垂足为E、F,连接OA,OC。
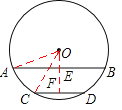
∵AB=30,CD=16,∴AE=![]() AB=15,CF=
AB=15,CF=![]() CD=8。
CD=8。
又∵⊙O的半径为17,即OA=OC=17。
∴在Rt△AOE中,![]() 。
。
在Rt△OCF中,![]() 。
。
∴EF=OF-OE=15-8=7。
答:AB和CD的距离为7cm。
【解析】垂径定理,;勾股定理。
分别作弦AB、CD的弦心距,设垂足为E、F;由于AB∥CD,则E、O、F三点共线,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,可连接OA、ODC在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
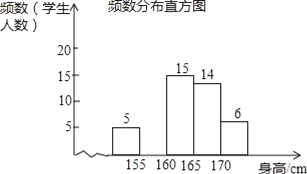
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
【题目】已知一圆形零件的标准直径是![]() ,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
序号 |
|
|
|
|
|
直径长度/ |
|
|
|
|
|
(1)试指出哪件样品的大小最符合要求?
(2)如果规定误差的绝对值在![]() 之内是正品.误差的绝对值在
之内是正品.误差的绝对值在![]() 之间是次品,误差的绝对值超过
之间是次品,误差的绝对值超过![]() 的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?
的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?