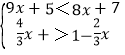题目内容
【题目】我们把1°的圆心角所对的弧叫做1°的弧,则圆心角AOB的度数等于它所对的弧AB的度数记为:∠AOB![]()
![]() .由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图形1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题(1)和问题(2).
.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,请结合图形1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题(1)和问题(2).
问题(1):如图2,⊙O的两条弦AB、CD相交于圆内一点P,求证:∠APC![]()
![]() (
(![]() +
+![]() );
);
问题(2):如图3,⊙O的两条弦AB、CD相交于圆外一点P,问题(1)中的结论是否成立,如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明)

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据圆周角的度数等于其所对的弧的度数的一半,得∠AOB,连BC,可证得∠APC![]()
![]() ;
;
(2)问题(1)中的结论不成立,连BC,可以得到类似的结论为:∠APC![]()
![]() .
.
试题解析:∵∠APB=![]() ∠AOB,又∵∠AOB
∠AOB,又∵∠AOB![]()
![]() ,∴∠APB
,∴∠APB![]()
![]()
![]() ,即圆周角的度数等于其所对的弧的度数的一半;
,即圆周角的度数等于其所对的弧的度数的一半;
问题(1)连BC,则∠APC=∠PCB+∠PBC,
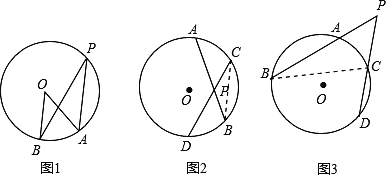
∵∠PCB的度数等于弧BD的度数的一半,∠PBC的度数等于弧AC的度数的一半,
∴∠APC![]()
![]() ;
;
问题(2):问题(1)中的结论不成立,
类似的结论为:∠APC![]()
![]() ,
,
连接BC,则∠APC=∠BCD∠PBC,
∵∠BCD的度数等于弧BD的度数的一半,∠PBC的度数等于弧AC的度数的一半,
∴∠APC![]()
![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目