ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌCЮЊЁЯAOBЕФБпOAЩЯвЛЕуЃЌOC=6ЃЌNЮЊБпOBЩЯвьгкЕуOЕФвЛЖЏЕуЃЌPЪЧЯпЖЮCNЩЯвЛЕуЃЌЙ§ЕуPЗжБ№зїPQЁЮOAНЛOBгкЕуQЃЌPMЁЮOBНЛOAгкЕуMЃЎ
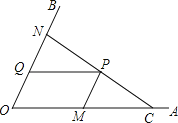
ЃЈ1ЃЉШєЁЯAOB=45ЁуЃЌOM=4ЃЌOQ=![]() ЃЌЧѓжЄЃКCNЁЭOBЃЛ
ЃЌЧѓжЄЃКCNЁЭOBЃЛ
ЃЈ2ЃЉЕБЕуNдкБпOBЩЯдЫЖЏЪБЃЌЫФБпаЮOMPQЪМжеБЃГжЮЊСтаЮЃЎ
ЂйЮЪЃК![]() ЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧѓГіЦфШЁжЕЗЖЮЇЃЛШчЙћВЛБфЃЌЧыЫЕУїРэгЩЃЛ
ЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШчЙћБфЛЏЃЌЧѓГіЦфШЁжЕЗЖЮЇЃЛШчЙћВЛБфЃЌЧыЫЕУїРэгЩЃЛ
ЂкЩшСтаЮOMPQЕФУцЛ§ЮЊS1ЃЌЁїNOCЕФУцЛ§ЮЊS2ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйВЛЛсБфЛЏЃЌМћНтЮіЃЌЂк0ЃМ![]() ЃМ
ЃМ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§PзїPEЁЭOAгкEЃЌNFЁЭOAЃЌЯШХаЖЯЫФБпаЮOMPQЮЊЦНааЫФБпаЮЃЌдйгУШёНЧШ§НЧКЏЪ§ЧѓГіЁЯPCE=45ЁуЃЌМДПЩЃЛ
ЃЈ2ЃЉЂйгЩЫФБпаЮOQPMЪЧСтаЮЃЌЩшOM=xЃЌON=yЃЌдђгаOQ=QP=OM=xЃЌNQ=y-xЃЌгЩЯрЫЦШ§НЧаЮЕФХаЖЈПЩжЄЁїNQPЁзЁїNOCЃЌМД![]() ЃЌМЬЖјМДПЩЕУ
ЃЌМЬЖјМДПЩЕУ![]() ЕФжЕВЛЗЂЩњБфЛЏЃЛ
ЕФжЕВЛЗЂЩњБфЛЏЃЛ
ЂкЙ§PзїPEЁЭOAЃЌЙ§NзїNFЁЭOAЃЌЯШХаЖЯГіЁїCPMЁзЁїCNOдйЕУЕНБШР§ЪН![]() ЃЌЧѓНтМДПЩЃЎ
ЃЌЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ
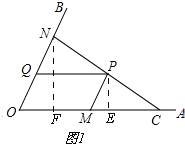
Й§PзїPEЁЭOAгкEЃЌNFЁЭOAЃЌ
ЁпPQЁЮOAЃЌPMЁЮOBЃЌ
ЁрЫФБпаЮOMPQЮЊЦНааЫФБпаЮЃЌ
ЁрPM=OQ= ![]() ЃЌЁЯPME=ЁЯAOB=45ЁуЃЌ
ЃЌЁЯPME=ЁЯAOB=45ЁуЃЌ
ЁрPE=PMsin45Ёу=1ЃЌME=1ЃЌ
ЁрCE=OCЃOMЃME=1ЃЌ
ЁрtanЁЯPCE= ![]() =1ЃЌ
=1ЃЌ
ЁрЁЯPCE=45ЁуЃЌ
ЁрЁЯCNO=90ЁуЃЌ
ЁрCNЁЭOBЃЛ
ЃЈ2ЃЉЂй![]() ЕФжЕВЛЗЂЩњБфЛЏЃЌ
ЕФжЕВЛЗЂЩњБфЛЏЃЌ
РэгЩЃКЩшOM=xЃЌON=yЃЌ
ЁпЫФБпаЮOMPQЮЊСтаЮЃЌ
ЁрOQ=QP=OM=xЃЌNQ=y-xЃЌ
ЁпPQЁЮOAЃЌ
ЁрЁЯNQP=ЁЯOЃЌ
ЁпЁЯQNP=ЁЯONCЃЌ
ЁрЁїNQPЁзЁїNOCЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр6yЃ6x=xyЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЂкШчЭМ2ЃЌ
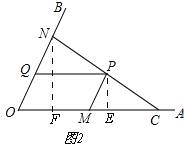
Й§PзїPEЁЭOAЃЌЙ§NзїNFЁЭOAЃЌ
ЁрS1=OMЁСPEЃЌS2= ![]() OCЁСNFЃЌ
OCЁСNFЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпPMЁЮOBЃЌ
ЁрЁЯPMC=ЁЯNOCЃЌ
ЁпЁЯPCM=ЁЯNCOЃЌ
ЁрЁїCPMЁзЁїCNOЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёп0ЃМxЃМ6ЃЌ
Ёр0ЃМ![]() ЃМ
ЃМ![]() ЃЎ
ЃЎ

 жЧШЄКЎМйзївЕдЦФЯПЦММГіАцЩчЯЕСаД№АИ
жЧШЄКЎМйзївЕдЦФЯПЦММГіАцЩчЯЕСаД№АИЁОЬтФПЁПФГвЉЦЗЩњВњЛљЕиЙВга5ЬѕЩњВњЯпЃЌУПЬѕЩњВњЯпУПдТЩњВњвЉЦЗ20ЭђКаЃЌИУЛљЕиДђЫуДгЕквЛИідТПЊЪМЕНЕкЮхИідТНсЪјЃЌЖдУПЬѕЩњВњЯпНјааЩ§МЖИФдьЃЎИФдьЪБЃЌУПИідТжЛЩ§МЖИФдьвЛЬѕЩњВњЯпЃЌетЬѕЩњВњЯпЕБдТЭЃВњЃЌВЂгкЯТИідТЭЖШыЩњВњЃЌЦфЫћЩњВњЯпдђе§ГЃЩњВњЃЎОЕїВщЃЌУПЬѕЩњВњЯпЩ§МЖИФдьКѓЃЌУПдТЕФВњСПЛсБШдРДЬсИп20%ЃЎ
ЃЈ1ЃЉИљОнЬтвтЃЌЭъГЩЯТУцЮЪЬтЃК
ЂйАбЯТБэВЙГфЭъећЃЈжБНгаДдкКсЯпЩЯЃЉЃК
дТЪ§ | Ек1ИідТ | Ек2ИідТ | Ек3ИідТ | Ек4ИідТ | Ек5ИідТ | Ек6ИідТ | Ё |
ВњСП/ЭђКа | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | 92 | Ё | Ё | Ё |
ЂкДгЕк1ИідТНјааЩ§МЖИФдьКѓЃЌЕкЁЁ ЁЁИідТЕФВњСППЊЪМГЌЙ§ЮДЩ§МЖИФдьЪБЕФВњСПЃЛ
ЃЈ2ЃЉШєИУЛљЕиЕкxИідТЃЈ1ЁмxЁм5ЃЌЧвxЪЧећЪ§ЃЉЕФВњСПЮЊyЭђКаЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉвбжЊУПЬѕЩњВњЯпЕФЩ§МЖИФдьЗбЪЧ30ЭђдЊЃЌУПКавЉЦЗПЩЛёРћ3дЊЃЎЩшДгЕк1ИідТПЊЪМЩ§МЖИФдьКѓЃЌЩњВњвЉЦЗЫљЛёзмРћШѓЮЊW1ЭђдЊЃЛЭЌЪБЦкФкЃЌВЛЩ§МЖИФдьЫљЛёзмРћШѓЮЊW2ЭђдЊЩшжСЩйЕНЕкnИідТЃЈnЮЊе§ећЪ§ЃЉЪБЃЌW1ДѓгкW2ЃЌЧѓnЕФжЕЃЎЃЈРћШѓЃНЛёРћЉИФдьЗбЃЉ