题目内容
【题目】已知,点P是正方形ABCD内的一点,连PA、PB、PC.
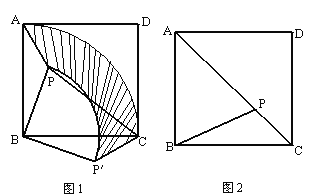
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积;
②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
【答案】(1)①S阴影=![]()
②连结PP′,证△PBP′为等腰直角三角形,从而PC=6;
- 将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,
- 再证∠BPC+∠APB=180°,即点P在对角线AC上.
【解析】(1)△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积实际是大扇形OAC与小扇形BPP′的面积差,且这两个扇形的圆心角同为90度;
(2)连接PP′,证△PBP′为等腰直角三角形,从而可在Rt△PP′C中,用勾股定理求得PC=6;
(3)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目