题目内容
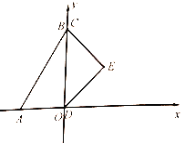
【题目】如图1,已知直线![]() 交
交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,平行于
两点,平行于![]() 轴的直线
轴的直线![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度向
个单位的速度向![]() 轴的负方向运动,直线
轴的负方向运动,直线![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设直线
,设直线![]() 的运动时间为
的运动时间为![]() 秒.
秒.

![]() 求线段
求线段![]() 的长.
的长.
![]() 若
若![]() 为直线
为直线![]() 上一动点,将
上一动点,将![]() 沿着
沿着![]() 翻折,当点
翻折,当点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上时,求直线
上时,求直线![]() 的解析式.
的解析式.
![]() 若
若![]() 为
为![]() 的中点,当
的中点,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
【答案】(1)AB=6;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)首先求出点A、B的坐标,然后利用勾股定理即可得出AB;
(2)首先根据题意得出点C坐标,然后根据折叠的性质求出直线PC′的解析式,进而得出点P坐标,即可得出直线AP解析式;
(3)分情况讨论:①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时;根据坐标求两点间距离构造方程,即可得解.
时;根据坐标求两点间距离构造方程,即可得解.
![]() 由题意,得当
由题意,得当![]() ,
,![]() ,即
,即![]() ,
,
当![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
∴![]()
∴![]()
![]() 如图所示:
如图所示:
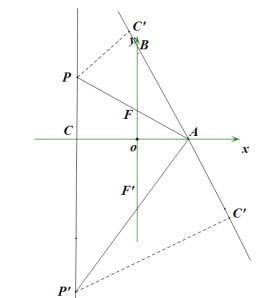
由题意,得点C坐标为![]() ,∠ACP=∠AC′P=90°
,∠ACP=∠AC′P=90°
∴AC=4
∵C′在直线AB上,设C′![]()
∴AC′=AC=![]() =4
=4
解得![]() 或
或![]()
∴C′坐标为![]() 或
或![]()
∵PC′⊥AC′
∴设直线PC′解析式为![]() ,将C′坐标代入,得
,将C′坐标代入,得
![]() 或
或![]()
∴点P坐标为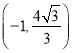 或
或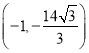
设直线AP解析式为![]() ,将点A、P代入,得
,将点A、P代入,得
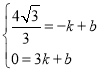 或
或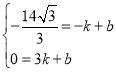
解得 或
或
∴直线![]() 的解析式为
的解析式为![]() 或
或![]() ;
;
![]() ①当
①当![]() 时,作BE⊥DP,如图所示,
时,作BE⊥DP,如图所示,
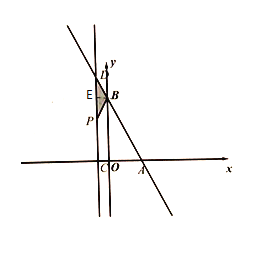
∵点P为CD中点
∴E为DP中点
∴![]() ,即
,即![]()
∴![]() ;
;
②当![]() 时,如图所示:
时,如图所示:
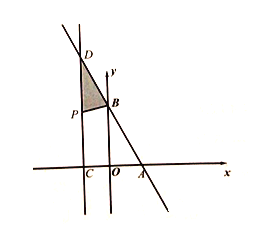
设点D坐标为![]() ,则点P坐标为
,则点P坐标为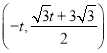
∴
解得![]() 或
或![]() (舍去)
(舍去)
∴![]() ;
;
③当![]() 时,如图所示:
时,如图所示:
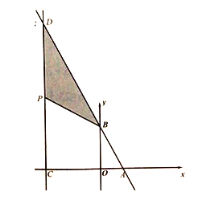
设点D坐标为![]() ,则点P坐标为
,则点P坐标为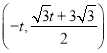
∴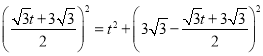
解得![]()
∴![]()
综上所述,![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目