题目内容
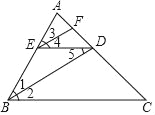
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.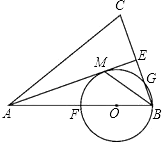
(1)求证:AE与⊙O相切;
(2)当BC=4,AC=6,求⊙O的半径.
【答案】
(1)解:证明:连接OM,
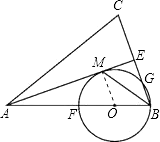
则∠OMB=∠OBM=∠MBE
又∵AB=AC,AE是角平分线,
∴AE⊥BC,
∴∠OMB+∠BME=∠MBE+∠BME=90°,∴∠AMO=90°,
∴AE与⊙O相切
(2)解:由AE与⊙O相切,AE⊥BC
∴OM∥BC
∴△AOM∽△ABE
∴ ![]()
∵BC=4
∴BE=2,AB=6,
即 ![]() ,
, ![]()
【解析】(1)连接OM ,根据角平分线的定义及等边对等角得出∠OMB=∠OBM=∠MBE,根据等腰三角形的三线合一得出AE⊥BC,根据三角形的内角和及等量代换得出∠AMO=90°,从而得出结论AE与⊙O相切 ;
(2)根据切线的性质定理及平行线的判定方法得出OM∥BC,根据平行于三角形一边的直线截其它两边所截得的三角形与原三角形相似得△AOM∽△ABE;根据相似三角形对应边成比例得出OM∶BE=AO∶AB ;从而得出关于圆的半径的方程,求解即可。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?