题目内容
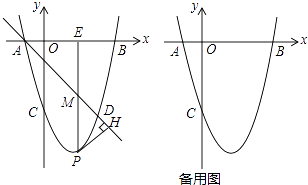
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= ![]() .
.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
【答案】
(1)解:∵点A的坐标为(﹣1,0),
∴OA=1.
又∵tan∠ACO= ![]() ,
,
∴OC=4.
∴C(0,﹣4).
∵OC=OB,
∴OB=4
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x﹣4).
∵将x=0,y=﹣4代入得:﹣4a=﹣4,解得a=1,
∴抛物线的解析式为y=x2﹣3x﹣4
(2)解:∵抛物线的对称轴为x=﹣ ![]() =
= ![]() ,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
∴D(3,﹣4).
设直线AD的解析式为y=kx+b.
∵将A(﹣1,0)、D(3,﹣4)代入得: ![]() ,解得k=﹣1,b=﹣1,
,解得k=﹣1,b=﹣1,
∴直线AD的解析式y=﹣x﹣1.
∵直线AD的一次项系数k=﹣1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°.
∴∠PMH=∠AME=45°.
∴△MPH的周长=PM+MH+PH=PM+ ![]() MP+
MP+ ![]() PM=(1+
PM=(1+ ![]() )PM.
)PM.
设P(a,a2﹣3a﹣4),M(﹣a﹣1),则PM=﹣a﹣1﹣(a2﹣3a﹣4)=﹣a2+2a+3,
∵PM=﹣a2+2a+3=﹣(a﹣1)2+4,
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=4×(1+ ![]() )=4+4
)=4+4 ![]()
(3)解:如图1所示;当∠EGN=90°.
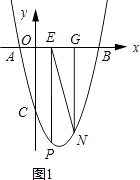
设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴ ![]() 时,△AOC∽△EGN.
时,△AOC∽△EGN.
∴ ![]() =
= ![]() ,整理得:a2+a﹣8=0.
,整理得:a2+a﹣8=0.
解得:a= ![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为( ![]() ,0).
,0).
如图2所示:当∠EGN=90°.
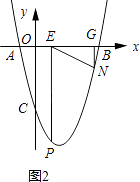
设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴ ![]() 时,△AOC∽△NGE.
时,△AOC∽△NGE.
∴ ![]() =4,整理得:4a2﹣11a﹣17=0.
=4,整理得:4a2﹣11a﹣17=0.
解得:a= ![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为( ![]() ,0).
,0).
∵EN在EP的右面,
∴∠NEG<90°.
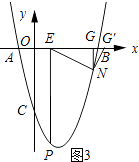
如图3所示:当∠ENG′=90°时,
EG′=EG× ![]() ×
× ![]() =(
=( ![]() ﹣1)×
﹣1)× ![]() =
= ![]() .
.
∴点G′的横坐标= ![]() .
.
∵ ![]() ≈4.03>4,
≈4.03>4,
∴点G′不在EG上.
故此种情况不成立.
综上所述,点G的坐标为( ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,-4),然后利用待定系数法可求得直线AD的解析式,根据直线AD的一次项系数的特点得出∠BAD=45°,进而得出△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2-3a-4),M(-a-1),则PM=-a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=(![]() )PM,即可以得出答案;
)PM,即可以得出答案;
(3)当∠EGN=90°时,设点G的坐标为(a,0),则N(a,a2-3a-4),则EG=a-1,NG=-a2+3a+4,故OA∶OC=EG∶GN ;如果△AOC∽△EGN,然后根据题意列方程求解判断是否适合题意即可 。’
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和二次函数的最值的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?