题目内容
如图,⊙O的直径AB=12cm,AM、BN是两条切线,DC切⊙O于E,交AM于D,交BN于C,设AD=x,
BC=y。
BC=y。

(1)求y与x的函数关系式,并说明是什么函数?
(2)若x、y是方程2t2-30t+m=0的两根,求△COD的面积;
(3)在(2)的条件下,以B为坐标原点,BC为x轴的正半轴, BA为y轴的正半轴,建立坐标系,求直线CD的解析式。
(2)若x、y是方程2t2-30t+m=0的两根,求△COD的面积;
(3)在(2)的条件下,以B为坐标原点,BC为x轴的正半轴, BA为y轴的正半轴,建立坐标系,求直线CD的解析式。
解:(1)过点D作DF⊥BC,垂足为F,则四边形ABFD为矩形,
∵⊙O切AM、BN、CD于A、B、E,
∴DE=AD,CE=CB,
∵AD=x,CB=y,
∴CF=y-x,CD=x+y,
在Rt△DCF中,
DC2=DF2+CF2,即(x+y)2=(x-y)2+122,
∴xy=36,
∴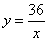 为反比例函数。
为反比例函数。
(2)由x、y是方程2t2-30t+m=0的两根,可得:
x+y=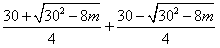 =15,
=15,
同理可得:xy=36,
∴x=3,y=12或x=12,y=3,
连结OE,则OE⊥CD,
∴S△COD=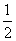 CD·OE=
CD·OE= ×(AD+BC)·
×(AD+BC)·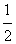 AB =
AB =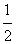 ×15×
×15× ×12 =45cm2。
×12 =45cm2。
(3)由(2)知AD=3,BC=12或AD=12,BC=3,则D(3,12)或(12,12),
C(12,0)或(3,0),
故可求直线CD的解析式为:
y=-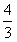 x+16或y=
x+16或y=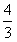 x+4。
x+4。
∵⊙O切AM、BN、CD于A、B、E,
∴DE=AD,CE=CB,
∵AD=x,CB=y,
∴CF=y-x,CD=x+y,
在Rt△DCF中,
DC2=DF2+CF2,即(x+y)2=(x-y)2+122,
∴xy=36,
∴
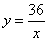 为反比例函数。
为反比例函数。(2)由x、y是方程2t2-30t+m=0的两根,可得:
x+y=
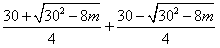 =15,
=15,同理可得:xy=36,
∴x=3,y=12或x=12,y=3,
连结OE,则OE⊥CD,
∴S△COD=
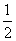 CD·OE=
CD·OE= ×(AD+BC)·
×(AD+BC)·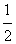 AB =
AB =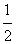 ×15×
×15× ×12 =45cm2。
×12 =45cm2。(3)由(2)知AD=3,BC=12或AD=12,BC=3,则D(3,12)或(12,12),
C(12,0)或(3,0),
故可求直线CD的解析式为:
y=-
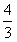 x+16或y=
x+16或y=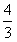 x+4。
x+4。
练习册系列答案
相关题目
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是