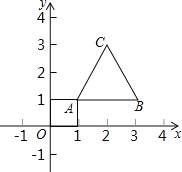题目内容
【题目】如图所示，一圆弧过方格的格点A，B，C，在方格中建立平面直角坐标系，使点A的坐标为(－2，4).
(1) 用直尺画出该圆弧所在圆的圆心M的位置，并写出点M的坐标；
(2)判断点D与⊙M的位置关系，并说明理由．
【答案】(1) (－1，1);(2) 见解析.
【解析】
（1）由点A的坐标为（-2，4）可知，x轴在点A的下方4个单位处，y轴在点A的右边2个单位长度处，由此建立其坐标系，然后连接AB、AC，分别画出线段AB和AC的垂直平分线，两条垂直平分线的交点就是所求的点M，然后写出点M的坐标即可；
（2）根据（1）中所得点M的坐标和已知的点A的坐标计算出圆M的半径MA的长，结合点D的坐标和点M的坐标求出MD的长，比较MA和MD的大小即可得出点D与圆M的位置关系.
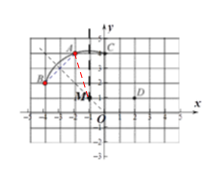
(1)建立的平面直角坐标系和圆心M的位置如下图所示，
由图可得：圆心M的坐标为(－1，1) ；
(2) 如下图，连接MA，
∵A的坐标为（-2，4），点M的坐标为（-1，1），
∴⊙M的半径MB=
，
∵点D的坐标为：(2，1)，
∴MD=3，
∵3＜，
∴点D在⊙M内.
阅读快车系列答案
【题目】温州某企业安排65名工人生产甲、乙两种产品，每人每天生产2件甲或1件乙，甲产品每件可获利15元．根据市场需求和生产经验，乙产品每天产量不少于5件，当每天生产5件时，每件可获利120元，每增加1件，当天平均每件获利减少2元．设每天安排x人生产乙产品．
（1）根据信息填表
产品种类 | 每天工人数（人） | 每天产量（件） | 每件产品可获利润（元） |
甲 | 15 | ||
乙 |
|
|
（2）若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元，求每件乙产品可获得的利润．
（3）该企业在不增加工人的情况下，增加生产丙产品，要求每天甲、丙两种产品的产量相等．已知每人每天可生产1件丙（每人每天只能生产一件产品），丙产品每件可获利30元，求每天生产三种产品可获得的总利润W（元）的最大值及相应的x值．
