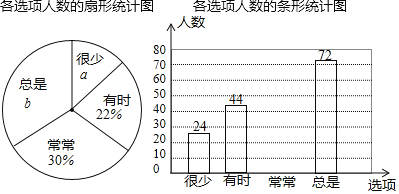
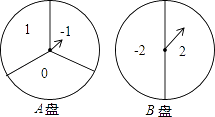
��Ŀ����
����Ŀ����ͼ������ABCD�����߳�AB=18cm��AD=4cm����P��Q�ֱ��A��Bͬʱ������P�ڱ�AB����AB������ÿ��2cm���ٶ������˶���Q�ڱ�BC����BC������ÿ��1cm���ٶ������˶�����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊx�룬��PBQ�����Ϊy��cm2���� 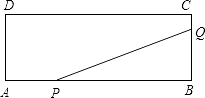
��1����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2�����PBQ����������ֵ��
���𰸡�
��1���⣺��S��PBQ= ![]() PBBQ��PB=AB��AP=18��2x��BQ=x��
PBBQ��PB=AB��AP=18��2x��BQ=x��
��y= ![]() ��18��2x��x��
��18��2x��x��
��y=��x2+9x��0��x��4��
��2���⣺�ɣ�1��֪��y=��x2+9x��
��y=����x�� ![]() ��2+
��2+ ![]() ��
��
�ߵ�0��x�� ![]() ʱ��y��x�����������
ʱ��y��x�����������
��0��x��4��
�൱x=4ʱ��y���ֵ=20��
����PBQ����������20cm2
����������1���ֱ��ʾ��PB��BQ�ij���Ȼ����������ε������ʽ��ʽ�������ɵý⣻��2���Ѻ�����ϵʽ�����ɶ���ʽ����ʽ��Ȼ����ݶ��κ�������ֵ������
�����㾫�������ڱ��⿼��Ķ��κ�������ֵ�;��ε����ʣ���Ҫ�˽�����Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a�����ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����Ȳ��ܵó���ȷ�𰸣�

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�