题目内容
【题目】规定两数
、
之间的一种运算，记作（，）；如果
，那么（，）=c.
例如:因为
，所以（2，8）=3.
(1)根据上述规定，填空:（4，16）=_________，（7，1）=___________，（_______，
）=-2.
(2)小明在研究这种运算时发现一个现象:（
，
）=（3，4）小明给出了如下的证明:
设（，）=
，则
，即
所以
，即（3，4）=，
所以（，）=（3，4）.
请你尝试运用这种方法解决下列问题:
①证明:（6，45）-（6，9）=（6，5）
②猜想:（
，
）+（
，
）=（____________，____________），(结果化成最简形式).
【答案】（1）2，0，5；
（2）①证明见解析；②（x+1），（y2-3y+2）．
【解析】
（1）根据规定的两数之间的运算法则解答；
（2）①根据同底数幂的乘法法则，结合定义证明；②根据例题和①中证明的式子作为公式进行变形即可．
（1）因为42=16，所以【4，16】=2．
因为70=1，所以【7，1】=0．
因为5-2=
，所以【5，】=-2．
故答案为：2，0，5；
（2）①证明：设【6，9】=x，【6，5】=y，则6x=9，6y=5，
∴5×9=45=6x6y=6x+y，
∴【6，45】=x+y，
则：【6，45】=【6，9】+【6，5】，
∴【6，45】-【6，9】=【6，5】；
②∵【3n，4n】=【3，4】，
∴【（x+1）m，（y-1）m】=【（x+1），（y-1）】，【（x+1）n，（y-2）n】=【（x+1），（y-2）】，
∴【（x+1）m，（y-1）m】+【（x+1）n，（y-2）n】，
=【（x+1），（y-1）】+【（x+1），（y-2）】，
=【（x+1），（y-1）（y-2）】，
=【（x+1），（y2-3y+2）】．
故答案为：（x+1），（y2-3y+2）．
【题目】学校为了让同学们走向操场、积极参加体育锻炼，启动了“学生阳光体育运动”，张明和李亮在体育运动中报名参加了百米训练小组．在近几次百米训练中，教练对他们两人的测试成绩进行了统计和分析，请根据图表中的信息解答以下问题：
平均数 | 中位数 | 方差 | |
张明 | 13.3 | 0.004 | |
李亮 | 13.3 | 0.02 |
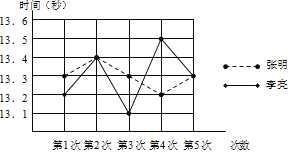
（1）张明第2次的成绩为： 秒；
（2）张明成绩的平均数为： ；李亮成绩的中位数为： ；
（3）现在从张明和李亮中选择一名成绩优秀的去参加比赛，若你是他们的教练，应该选择谁？请说明理由．
