题目内容
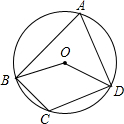
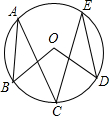
如图A，B，C，D四点在同一圆周上，且BC=DC=4，AE=6，线段BE、DE的长为正整数，求BD的长．
∵BC=CD，
∴∠BAC=∠DAC，
∵∠DBC=∠DAC，
∴∠BAC=∠DBC，
又∵∠BCE=∠ACB，
∴△ABC∽△BEC，
∴BC2=CE•AC，
∵BC=CD=4，AE=6，
∴EC=2，
由相交弦定理得，BE•DE=AE•EC，
即BE•DE=12，
又线段BE、ED为正整数，
且在△BCD中，BC+CD＞BE+DE，
所以可得BE=3、DE=4或BE=4、DE=3，
所以BD=BE+DE=7．
故答案为：7．
∴∠BAC=∠DAC，
∵∠DBC=∠DAC，
∴∠BAC=∠DBC，
又∵∠BCE=∠ACB，
∴△ABC∽△BEC，
∴BC2=CE•AC，
∵BC=CD=4，AE=6，
∴EC=2，
由相交弦定理得，BE•DE=AE•EC，
即BE•DE=12，
又线段BE、ED为正整数，
且在△BCD中，BC+CD＞BE+DE，
所以可得BE=3、DE=4或BE=4、DE=3，
所以BD=BE+DE=7．
故答案为：7．
练习册系列答案
阅读快车系列答案
相关题目
