题目内容
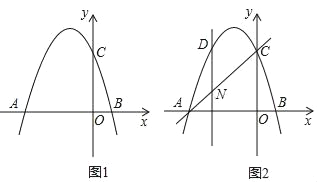
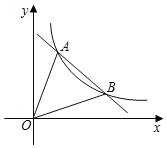
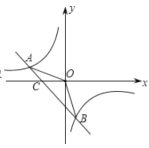
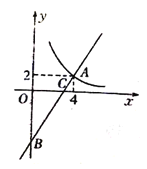
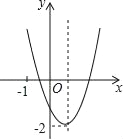
【题目】已知,二次函数y=ax2+bx+c满足以下三个条件:①![]() >4c,②a﹣b+c<0,③b<c,则它的图象可能是( )
>4c,②a﹣b+c<0,③b<c,则它的图象可能是( )
A.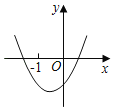 B.
B.
C.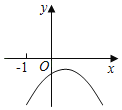 D.
D.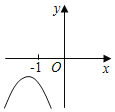
【答案】D
【解析】
由抛物线满足②a-b+c<0,③b<c,可得出a<0,只能在C、D中选择,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
∵a-b+c<0,b<c
∴a<b-c<0
抛物线开口向下,故A、B不符合题意
C.∵对称轴直线x=﹣![]() >0,a<0,∴b>0,
>0,a<0,∴b>0,
∵抛物线交y的负半轴,∴c<0,∴b>c,故C不符合题意;
D. ∵对称轴直线x=﹣![]() <-1,a<0,∴b<0,
<-1,a<0,∴b<0,
∵抛物线交y的负半轴,∴c<0
∵抛物线与x轴无交点,
∴b2-4ac<0
∴![]() >4c,
>4c,
由图像可知当x=-1时,a﹣b+c<0
,故D符合题意;
故选:D.

练习册系列答案
相关题目