题目内容
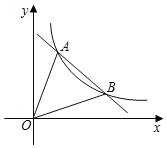
【题目】如图所示,双曲线y=![]() (x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(x>0,k>0)与直线y=ax+b(a≠0,b为常数)交于A(2,4),B(m,2)两点.
(1)求m的值;
(2)若C点坐标为(n,0),当AC+BC的值最小时,求出n的值;
(3)求△AOB的面积.
【答案】(1)m=4;(2)n=![]() ;(3)6.
;(3)6.
【解析】
(1)由A点坐标即可求出反比例函数,再把B点坐标代入反比函数即可求出m的值;
(2)求得B点关于x轴的对称点B′(4,-2),连接AB′,交x轴与C,此时AC+BC=AB′,AC+BC的值最小,根据待定系数法求得直线AB′的解析式,然后把(n,0)代入求得的解析式即可求得n的值;
(3)根据待定系数法求得直线AB的解析式,即可得到直线AB与x轴的交点C的坐标,然后根据S△AOB=S△AOC-S△BOC求得即可.
解:(1)把A(2,4)代入y=![]() (x>0,k>0),
(x>0,k>0),
∴k=2×4=8,
∴反比例函数的解析式为y=![]() ,
,
把B(m,2)代入y=![]() 得,2=
得,2=![]() ,
,
解得m=4;
(2)由(1)可知:A(2,4),B(4,2),
∴B点关于x轴的对称点B′(4,﹣2),
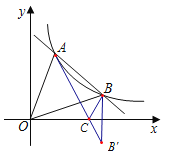
连接AB′,交x轴与C,此时AC+BC=AB′,AC+BC的值最小,
设直线AB′的解析式为y=ax+b,
把A(2,4),B′(4,﹣2)代入得![]() ,
,
解得:![]() ,
,
∴直线AB′的解析式为y=﹣3x+10,
把(n,0)代入得y=﹣3n+10,
∴n=![]() ;
;
(3)设直线AB的解析式为y=mx+t,
∴把A(2,4),B(4,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+6,
∴直线AB与x轴的交点C(6,0),
∴S△AOB=S△AOC﹣S△BOC=![]() ×6×4﹣
×6×4﹣![]() ×6×2=6.
×6×2=6.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目