Question

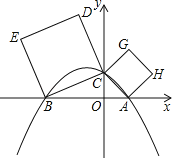
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a＜0）交x轴于A，B两点（B在A左侧），交y轴于点C，且CO＝AO，分别以BC，AC为边向外做正方形BCDE，正方形ACGH，记它们的面积分别为S1，S2，△ABC面积记为S3，当S1+S2＝6S3时，b的值为（　　）

A.B.C.D.

Answer 1

【答案】B

【解析】

根据题意即可求出点C和点A的坐标，利用勾股定理和面积的关系列出方程即可求出点B的坐标，设抛物线解析式为y＝a（x+9）（x﹣3），然后将点C的坐标代入即可求出a的值，变为一般式即可求出结论．

解：当x＝0时，y＝ax2+bx+3＝3，则C（0，3），

∴OC＝OA＝3，

∴A（3，0），

∵S1+S2＝6S3，

∴OC2+OB2+OC2+OA2＝6××3×（OB+3），

整理得OB2﹣9OB＝0，解得OB＝9，

∴B（﹣9，0），

设抛物线解析式为y＝a（x+9）（x﹣3），

把C（0，3）代入得a×9×（﹣3）＝3，解得a＝﹣，

∴抛物线解析式为y＝﹣（x+9）（x﹣3），

即y＝﹣x2﹣x+3，

∴b＝﹣．

故选：B．