Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ‘ń∂Ń”ŽňľŅľ£ļ
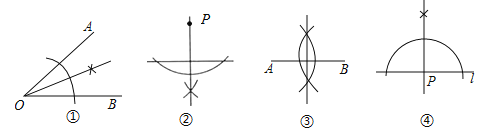
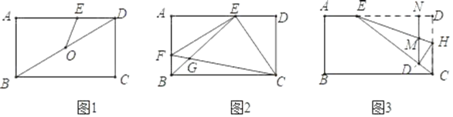
įĘĽý√◊Ķ¬£®Ļę‘™«į287ńÍ“ĽĻę‘™«į212ńÍ£©£¨őįīůĶńĻŇŌ£ņį’‹—ßľ“°ĘįŔŅ∆ ĹŅ∆—ßľ“°Ę ż—ßľ“°ĘőÔņŪ—ßľ“°ĘѶ—ßľ“£¨ĺ≤ըѶ—ßļÕŃųŐŚĺ≤Ѷ—ßĶńĶžĽý»ň£¨įĘĽý√◊Ķ¬Ńųīę”ŕ ņĶń÷Ý◊ų”–10”ŗ÷÷£¨∂ŗő™Ō£ņįőń ÷łŚŌ¬√ś «°∂įĘĽý√◊Ķ¬»ęľĮ°∑÷–ľ«‘ōĶń“ĽłŲ√ŁŐ‚£ļAB «°—OĶńŌ“£¨Ķ„C‘ŕ°—O…Ō£¨«“CD°ÕAB”ŕĶ„D£¨‘ŕŌ“AB…Ō»°Ķ„E£¨ ĻAD£ĹDE£¨Ķ„F «![]() …ŌĶń“ĽĶ„£¨«“
…ŌĶń“ĽĶ„£¨«“![]() £Ĺ
£Ĺ![]() £¨Ń¨Ĺ”BFŅ…Ķ√BF£ĹBE£ģ
£¨Ń¨Ĺ”BFŅ…Ķ√BF£ĹBE£ģ
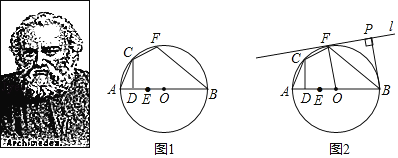
£®1£©Ĺę…Ō Ųő Ő‚÷–Ō“ABłńő™÷Īĺ∂AB£¨»ÁÕľ1ňý ĺ£¨ ‘÷§√ųBF£ĹBE£Ľ
£®2£©»ÁÕľ2ňý ĺ£¨»Ű÷Īĺ∂AB£Ĺ10£¨EO£Ĺ![]() OB£¨◊ų÷ĪŌŖl”Ž°—OŌŗ«–”ŕĶ„F£ģĻżĶ„B◊ųBP°Õl”ŕĶ„P£ģ«ůBPĶń≥§£ģ
OB£¨◊ų÷ĪŌŖl”Ž°—OŌŗ«–”ŕĶ„F£ģĻżĶ„B◊ųBP°Õl”ŕĶ„P£ģ«ůBPĶń≥§£ģ
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©Ń¨Ĺ”CE°ĘBC£¨÷§≥Ų°ųCEB°’°ųCFB£¨‘ÚŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£®2£©Ō»«ůBE≥§£¨÷§≥Ų°ųAFB°◊°ųFPB£¨Ķ√Ī»ņżŌŖ∂őľīŅ…«ů≥ŲBP≥§£ģ
£®1£©»ÁÕľ1ňý ĺ£¨Ń¨Ĺ”CE°ĘBC£¨
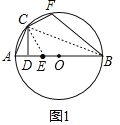
°ŖCD°ÕAB£¨AD£ĹDE£¨
°ŗAC£ĹCE£¨
°ŗ°ŌCAE£Ĺ°ŌCEA£¨
”÷°Ŗ![]() £¨
£¨
°ŗCA£ĹCF£¨°ŌFBC£Ĺ°ŌEBC£¨
°ŗCE£ĹCF£¨
”÷°Ŗ°ŌA+°ŌF£Ĺ180°„£¨°ŌCEA+°ŌCEB£Ĺ180°„£¨
°ŗ°ŌCEB£Ĺ°ŌF£¨
°ŗ°ųCEB°’°ųCFB£®AAS£©£¨
°ŗBE£ĹBF£Ľ
£®2£©»ÁÕľ2ňý ĺ£¨Ń¨Ĺ”AF£¨
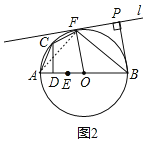
°ŖAB£Ĺ10£¨EO£Ĺ![]() £¨
£¨
°ŗEB£Ĺ7.5£¨
°ŖABő™°—OĶń÷Īĺ∂£¨
°ŗ°ŌAFB£Ĺ90°„£¨
°Ŗl”Ž”Ž°—OŌŗ«–”ŕĶ„F£¨
°ŗ°ŌOFP£Ĺ90°„£¨
°ŗ°ŌAFO£Ĺ°ŌBFP£¨
”÷°ŖOF£ĹOA£¨
°ŗ°ŌOAF£Ĺ°ŌOFA£¨
°ŗ°ŌOAF£Ĺ°ŌBFP£¨
°ŖBP°Õl”ŕĶ„P£¨
°ŗ°ŌBPF£Ĺ90°„£¨
°ŗ°ųAFB°◊°ųFPB£¨
![]() £¨
£¨
ľī![]() £¨
£¨
![]() £ģ
£ģ

 »ę”ŇĶ„Ń∑Ķ•‘™ľ∆ĽģŌĶŃ–īūįł
»ę”ŇĶ„Ń∑Ķ•‘™ľ∆ĽģŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ ‹Ķō’ūĶń”įŌž£¨ń≥≥¨ –ľ¶ĶįĻ©”¶ĹŰ’Ň£¨–Ť√ŅŐžī”Õ‚ĶōĶų‘ňľ¶Ķį1200ĹÔ£ģ≥¨ –ĺŲ∂®ī”ľ◊°Ę““ŃĹīů–Õ—Ý÷≥≥°Ķų‘ňľ¶Ķį£¨“—÷™ľ◊—Ý÷≥≥°√ŅŐž◊Ó∂ŗŅ…Ķų≥Ų800ĹÔ£¨““—Ý÷≥≥°√ŅŐž◊Ó∂ŗŅ…Ķų≥Ų900ĹÔ£¨ī”ŃĹ—Ý÷≥≥°Ķų‘ňľ¶ĶįĶĹ≥¨ –Ķń¬∑≥ŐļÕ‘ň∑—»ÁĪŪ£ļ
ĶĹ≥¨ –Ķń¬∑≥Ő(«ß√◊) | ‘ň∑—(‘™/ĹÔ«ß√◊) | |
ľ◊—Ý÷≥≥° | 200 | 0.012 |
““—Ý÷≥≥° | 140 | 0.015 |
(1)»Űń≥ŐžĶų‘ňľ¶ĶįĶń◊‹‘ň∑—ő™2670‘™£¨‘Úī”ľ◊°Ę““ŃĹ—Ý÷≥≥°łųĶų‘ňŃň∂ŗ…ŔĹÔľ¶Ķį£Ņ
(2)…Ťī”ľ◊—Ý÷≥≥°Ķų‘ňľ¶ĶįxĹÔ£¨◊‹‘ň∑—ő™W‘™£¨ ‘–ī≥ŲW”ŽxĶńļĮ żĻōŌĶ Ĺ£¨‘ű—ýį≤ŇŇĶų‘ň∑Ĺįł≤Ňń‹ Ļ√ŅŐžĶń◊‹‘ň∑—◊Ó °£Ņ
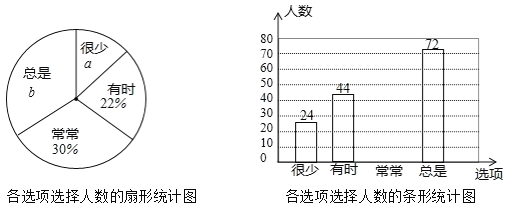
°ĺŐ‚ńŅ°Ņļž ųŃ÷—ß–£‘ŕ∆ŖńÍľ∂–¬…ķ÷–ĺŔ––Ńň»ę‘Ī≤őľ”Ķń°į∑ņńÁňģ°Īį≤»ę÷™ ∂ĺļ»Ł£¨ ‘ĺŪŐ‚ńŅĻ≤10Ő‚£¨√ŅŐ‚10∑÷£ģŌ÷∑÷Īūī”»żłŲįŗ÷–łųňśĽķ»°10√ŻÕ¨—ßĶń≥…ľ®£®Ķ•őĽ£ļ∑÷£©£¨ ’ľĮ żĺ›»ÁŌ¬£ļ
1įŗ£ļ90£¨70£¨80£¨80£¨80£¨80£¨80£¨90£¨80£¨100£Ľ
2įŗ£ļ70£¨80£¨80£¨80£¨60£¨90£¨90£¨90£¨100£¨90£Ľ
3įŗ£ļ90£¨60£¨70£¨80£¨80£¨80£¨80£¨90£¨100£¨100£ģ
’ŻņŪ żĺ›£ļ
∑÷ ż »ň ż įŗľ∂ | 60 | 70 | 80 | 90 | 100 |
1įŗ | 0 | 1 | 6 | 2 | 1 |
2įŗ | 1 | 1 | 3 |
| 1 |
3įŗ | 1 | 1 | 4 | 2 | 2 |
∑÷őŲ żĺ›£ļ
∆Ĺĺý ż | ÷–őĽ ż | ÷ŕ ż | |
1įŗ | 83 | 80 | 80 |
2įŗ | 83 |
|
|
3įŗ |
| 80 | 80 |
łý囓‘…Ō–ŇŌĘĽōīūŌ¬Ń–ő Ő‚£ļ
£®1£©«Ž÷ĪĹ”–ī≥ŲĪŪłŮ÷–![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©Ī»ĹŌ’‚»ż◊ť—ýĪĺ żĺ›Ķń∆Ĺĺý ż°Ę÷–őĽ żļÕ÷ŕ ż£¨ń„»Ōő™ńńłŲįŗĶń≥…ľ®Ī»ĹŌļ√£Ņ«ŽňĶ√ųņŪ”…£Ľ
£®3£©ő™Ńň»√—ß…ķ÷ō ”į≤»ę÷™ ∂Ķń—ßŌį£¨—ß–£ĹęłÝĺļ»Ł≥…ľ®¬ķ∑÷ĶńÕ¨—ßįš∑ĘĹĪ◊ī£¨ł√–£∆ŖńÍľ∂–¬…ķĻ≤570»ň£¨ ‘Ļņľ∆–Ť“™◊ľĪł∂ŗ…Ŕ’ŇĹĪ◊ī£Ņ