题目内容
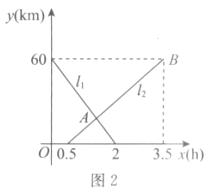
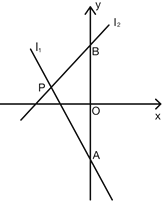
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距离A地的距离为y(km).甲车行驶的时间为x(h),y与x之间的函数图象如图所示.

(1)甲车从A地前往B地的速度为______km/h;
(2)求甲车返回时y与x之间的函数关系式;
(3)当甲、乙两车相距50km时,直接写出甲车行驶的时间.
【答案】(1)120;(2)![]() (2.5≤x≤5.5);(3)
(2.5≤x≤5.5);(3)![]() 小时,
小时,![]() 小时,
小时,![]() 小时.
小时.
【解析】
(1)根据函数图象中的数据可以求得甲车的速度;
(2)根据函数图象中的数据可以求得甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)根据“路程、速度、时间”的关系列方程解答即可.
(1)甲车的速度为:180÷1.5=120km/h,
故答案为:120;
(2)![]()
设甲车返回时y与x之间的函数关系式![]() ,
,
把![]() ,
,![]() 代入
代入![]() ,
,
解得![]()
![]()
![]() (2.5≤x≤5.5)
(2.5≤x≤5.5)
(3)乙甲的速度为:(300-180)÷1.5=80(千米/时),
由(2)得甲车返回时速度为100千米/时,
设甲、乙两车相距50km时,甲车行驶了x小时,根据题意得:
(120+80)x=300-50或(120+80)x=300+50或100(x-2.5)=250,
解得x=1.25或1.75或5.
答:当甲、乙两车相距50km时,甲车行驶的时间为1.25小时或1.75小时或5小时.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.