Question

【题目】如图，B处在A处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B处的北偏东80°方向，求∠ACB.

Answer 1

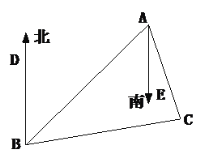
【答案】85°

【解析】

根据方向角的定义，可得∠BAE=45°，∠CAE=15°，∠DBC=80°，然后根据平行线的性质与三角形内角和定理即可求解．

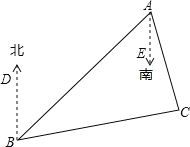
如图,根据方向角的定义,可得∠BAE=45°,∠CAE=15°,∠DBC=80°.

∵∠BAE=45°,∠EAC=15°，

∴∠BAC=∠BAE+∠EAC=45°+15°=60°.

∵AE，DB是正南正北方向，

∴BD∥AE，

∵∠DBA=∠BAE=45°，

又∵∠DBC=80°，

∴∠ABC=80°45°=35°，

∴∠ACB=180°∠ABC∠BAC=180°60°35°=85°.