题目内容
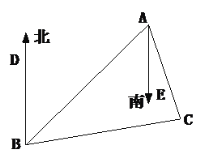
【题目】如图,等边![]() ,点
,点![]() 为射线
为射线![]() 上一点,延长
上一点,延长![]() 至点
至点![]() ,使得
,使得![]() ,联结
,联结![]() 并延长交射线
并延长交射线![]() 于点
于点![]() 。
。
(1)当点![]() 在边
在边![]() 上时,如图1,若
上时,如图1,若![]() ,则
,则![]()
(2)当点![]() 在边
在边![]() 上时,如图2,若
上时,如图2,若![]() ,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。
(3)当点![]() 在边
在边![]() 的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出
的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出![]() 与
与![]() 的数量关系并证明。
的数量关系并证明。

【答案】(1)60°;(2)见解析;(3)∠CFA+∠DBC=60°,理由见解析.
【解析】
(1)由等边三角形的性质可得BD⊥AE,∠DBE=∠DBA=30°,AB=AE,可求∠CFA=∠ABC+∠ECD=90°,即可求解;
(2)如图2,过点C作CH∥AB交AE的延长线于H,可证△CHE是等边三角形,可得CH=CE=HE=AD,通过证明△BAD≌△DHC,可得∠DBF=∠HDC,由外角性质可求解;
(3)如图3,过点C作CH∥AB交AE的延长线于H,可证△CHE是等边三角形,可得CH=CE=HE=AD,通过证明△BAD≌△DHC,可得∠DBF=∠HDC,由外角性质可求解;
(1)∵△ABE是等边三角形,ED=AD,
∴BD⊥AE,∠DBE=∠DBA=30°,AB=AE,
∵EC=AD,∠BEA=60°,
∴∠ECF=30°,
∴∠CFA=∠ABC+∠ECD=90°,
∴∠CFA-∠DBC=90°-30°=60°,
故答案为:60°;
(2)如图2,过点C作CH∥AB交AE的延长线于H,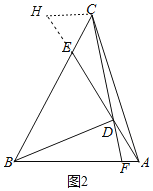
∵CH∥AB,
∴∠H=∠EAB=60°,∠HCE=∠EBA=60°,
∴△CHE是等边三角形,
∴CH=CE=HE,
∵EC=AD,
∴HE=CH=AD,
∴HE+DE=AD+DE,
∴HD=AE=AB,
∵HD=AB,AD=CH,∠H=∠BAD=60°,
∴△BAD≌△DHC(SAS)
∴∠DBF=∠HDC,
∵∠CFA=∠CBF+∠BCF=∠CBD+∠DBF+∠BCF,
∴∠CFA-∠DBC=∠DBF+∠BCF=∠HDC+∠BCF=∠BEA=60°;
(3)如图3,过点C作CH∥AB交AE的延长线于H,
∵CH∥AB,
∴∠HCD=∠CFA,∠H=∠EAB=60°,∠HCE=∠EBA=60°,
∴△CHE是等边三角形,
∴CH=CE=HE,
∵EC=AD,
∴HE=CH=AD,
∴HE-DE=AD-DE,
∴HD=AE=AB,
∵HD=AB,AD=CH,∠H=∠BAD=60°,
∴△BAD≌△DHC,(SAS)
∴∠DBA=∠HDC,∠HCD=∠BDA,
∴∠BDA=∠CFA,
∵∠AEB=∠ADB+∠DBC=60°,
∴∠CFA+∠DBC=60°.