Question

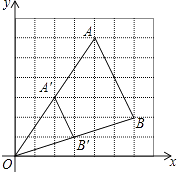
【题目】如图，在ABCD中，E、F分别是AB、CD的中点．

（1）求证：四边形EBFD为平行四边形；
（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．

Answer 1

【答案】
（1）

证明：∵四边形ABCD是平行四边形，

∴AB∥CD，AB=CD．

∵E、F分别是AB、CD的中点，

∴BE=DF，

∵BE∥DF，

∴四边形EBFD为平行四边形；

（2）

证明：∵四边形EBFD为平行四边形，

∴DE∥BF，

∴∠CDM=∠CFN．

∵四边形ABCD是平行四边形，

∴AB∥CD，AB=CD．

∴∠BAC=∠DCA，∠ABN=∠CFN，

∴∠ABN=∠CDM，

在△ABN与△CDM中，

，

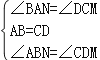∴△ABN≌△CDM （ASA）．

【解析】（1）根据平行四边形的性质：平行四边的对边相等，可得AB∥CD，AB=CD；根据一组对边平行且相等的四边形是平行四边形，可得答案；
（2）根据平行四边的性质：平行四边形的对边相等，可得AB∥CD，AB=CD，∠CDM=∠CFN；根据全等三角形的判定，可得答案．
【考点精析】关于本题考查的平行四边形的判定与性质，需要了解若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积才能得出正确答案．