题目内容
【题目】如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,点P在四边形ABCD的边上.若点P到BD的距离为
,点P在四边形ABCD的边上.若点P到BD的距离为![]() ,则点P的个数为( )
,则点P的个数为( )
A.2
B.3
C.4
D.5
【答案】A
【解析】过点A作AE⊥BD于E,过点C作CF⊥BD于F,∵∠BAD=∠ADC=90°,AB=AD=2![]() ,CD=
,CD=![]() ,∴∠ABD=∠ADB=45°,
,∴∠ABD=∠ADB=45°,
∴∠CDF=90°﹣∠ADB=45°,∵sin∠ABD=![]() ,∴AE=ABsin∠ABD=2
,∴AE=ABsin∠ABD=2![]() sin45°=2
sin45°=2![]()
![]() =2>
=2>![]() , CF=1<
, CF=1<![]()
所以在AB和AD边上有符合P到BD的距离为![]() 的点2个,故选A.
的点2个,故选A.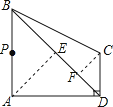
【考点精析】关于本题考查的等腰直角三角形和点到直线的距离,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;从直线外一点到这条直线的垂线段的长度叫做点到直线的距离才能得出正确答案.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
【题目】如图,在平面直角坐标系内,O为原点,点A的坐标为(﹣3,0),经过A、O两点作半径为![]() 的⊙C,交y轴的负半轴于点B.
的⊙C,交y轴的负半轴于点B.
(1)求B点的坐标;
(2)过B点作⊙C的切线交x轴于点D,求直线BD的解析式.
【题目】在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表,可以估计出n的值是 .




