题目内容
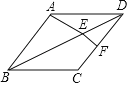
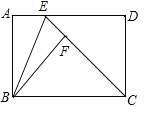
【题目】如图,矩形ABCD中,BC>AB,E是AD上一点,△ABE沿BE折叠,点A恰好落在线段CE的点F处,连结BF.
(1)求证:BC=CE;
(2)设![]() =k.
=k.
①若k=![]() ,求sin∠DCE的值;
,求sin∠DCE的值;
②设![]() =m,试求m与k满足的关系式.
=m,试求m与k满足的关系式.
【答案】(1)证明见解析;(2)①![]() ;②m2=2k﹣k2..
;②m2=2k﹣k2..
【解析】
(1)根据折叠的性质得到∠BEA=∠BEF,根据平行线的性质、等腰三角形的判定定理证明;
(2)①根据矩形的性质、正弦的定义计算;
②根据题意用AD表示出AB、AD,根据勾股定理列式计算即可.
(1)证明:由折叠的性质可知,∠BEA=∠BEF,
∵AD∥BC,
∴∠BEA=∠EBC,
∴∠BEF=∠EBC,
∴BC=CE;
(2)解:①∵![]() =
=![]() ,
,
∴AD=5AE,
∴DE=4AE,
∵BC=CE,
∴CE=5AE,
∴sin∠DCE=![]() =
=![]() ;
;
②∵![]() =k,
=k,![]() =m,
=m,
∴AE=kAD,AB=mAD,
∴DE=AD﹣AE=AD(1﹣k),
在Rt△CED中,CE2=CD2+DE2,即AD2=(mAD)2+[AD(1﹣k)]2,
整理得,m2=2k﹣k2.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目