题目内容
【题目】定义:若函数![]() 与
与![]() 轴的交点
轴的交点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,与
,与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,若
,若![]() ,
,![]() 中至少存在一个值,满足
中至少存在一个值,满足![]() (或
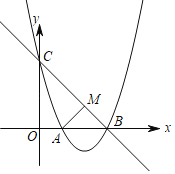
(或![]() ),则称该函数为友好函数.如图,函数
),则称该函数为友好函数.如图,函数![]() 与
与![]() 轴的一个交点
轴的一个交点![]() 的横坐标为-3,与
的横坐标为-3,与![]() 轴交点
轴交点![]() 的纵坐标为-3,满足
的纵坐标为-3,满足![]() ,称
,称![]() 为友好函数.
为友好函数.
(1)判断![]() 是否为友好函数,并说明理由;
是否为友好函数,并说明理由;
(2)请探究友好函数![]() 表达式中的
表达式中的![]() 与
与![]() 之间的关系;
之间的关系;
(3)若![]() 是友好函数,且
是友好函数,且![]() 为锐角,求
为锐角,求![]() 的取值范围.
的取值范围.
【答案】(1)是,理由见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() ,且
,且![]()
【解析】
(1)根据友好函数的定义,求出函数与x轴交点的横坐标以及与y轴交点的纵坐标,即可进行判断;
(2)先求出函数与y轴交点的纵坐标为c,再根据定义,可得当x=c时,y=0,据此可得出结果;
(3)分一下三种情况求解:(ⅰ)当![]() 在
在![]() 轴负半轴上时,由(2)可得:
轴负半轴上时,由(2)可得:![]() ,进而可得出结果;(ⅱ)当
,进而可得出结果;(ⅱ)当![]() 在
在![]() 轴正半轴上时,且
轴正半轴上时,且![]() 与
与![]() 不重合时,画出图像可得出结果;(ⅲ)当
不重合时,画出图像可得出结果;(ⅲ)当![]() 与原点重合时,不符合题意.
与原点重合时,不符合题意.
解:(1)![]() 是友好函数.理由如下:
是友好函数.理由如下:
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或3,
或3,
∴![]() 与
与![]() 轴一个交点的横坐标和与
轴一个交点的横坐标和与![]() 轴交点的纵坐标都是3.
轴交点的纵坐标都是3.
故![]() 是友好函数.
是友好函数.
(2)当![]() 时,
时,![]() ,即与
,即与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() .
.
∵![]() 是友好函数.
是友好函数.
∴![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上.
上.
代入得:![]() ,而
,而![]() ,∴
,∴![]() .
.
(3)(ⅰ)当![]() 在
在![]() 轴负半轴上时,由(2)可得:
轴负半轴上时,由(2)可得:![]() ,
,
即![]() ,显然当
,显然当![]() 时,
时,![]() ,
,
即与![]() 轴的一个交点为
轴的一个交点为![]() .
.
则![]() ,∴只需满足
,∴只需满足![]() ,即
,即![]() .
.
∴![]() .
.
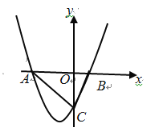
(ⅱ)当![]() 在
在![]() 轴正半轴上时,且
轴正半轴上时,且![]() 与
与![]() 不重合时,
不重合时,
∴显然都满足![]() 为锐角.
为锐角.
∴![]() ,且
,且![]() .
.
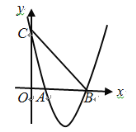
(ⅲ)当![]() 与原点重合时,不符合题意.
与原点重合时,不符合题意.
综上所述,![]() 或
或![]() ,且
,且![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目