题目内容
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).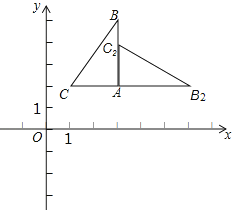
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2 , 点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
【答案】
(1)
解:A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,

(2)
解:
①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=![]() ,
,
∵![]() ,
,![]()
∴AB2+AC2=BC2,
∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,
∴旋转角为90°;
②∵AB=AB2=3,
∴CB2=AC+AB2=5,
∴B2的坐标为(6,2).
【解析】(1)分别得到点A、B、C关于x轴的对称点,连接点A1 , B1 , C1 , 即可解答;
(2)①根据点A,B,C的坐标分别求出AC,BC,AC的长度,根据勾股定理逆定理得到∠CAB=90°,即可得到旋转角;
②根据旋转的性质可知AB=AB2=3,所以CB2=AC+AB2=5,所以B2的坐标为(6,2).
【考点精析】根据题目的已知条件,利用作轴对称图形的相关知识可以得到问题的答案,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.

练习册系列答案
相关题目