Question

【题目】如图，曲线y1抛物线的一部分，且表达式为：y1=（x2﹣2x﹣3）（x≤3）曲线y2与曲线y1关于直线x=3对称．

（1）求A、B、C三点的坐标和曲线y2的表达式;
（2）过点D作CD∥x轴交曲线y1于点D，连接AD，在曲线y2上有一点M，使得四边形ACDM为筝形（如果一个四边形的一条对角线被另一条对角线垂直平分，这样的四边形为筝形），请求出点M的横坐标;
（3）设直线CM与x轴交于点N，试问在线段MN下方的曲线y2上是否存在一点P，使△PMN的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：在y1=（x2﹣2x﹣3）中，令y1=0，则有0=（x2﹣2x﹣3），解得x=﹣1或x=3，

∴A（﹣1，0），B（3，0），

又∵C为与y轴的交点，

∴C（0，），

又曲线y2与曲线y1关于直线x=3对称，

∴曲线y2可由曲线y1关向右平移3个单位得到，

∴y2=(X2-10X+21)（x≥3）

（2）

解：

若AD垂直平分CM，则可知CDMA为菱形，此时点M（1，0），显然不在y2上；

故直线CM垂直平分AD，取AD中点P，易求其坐标为（1，），

故直线CN的解析式为：yCN=x-，

求其与y2的交点坐标：，

解得：x1=，x2=（不合舍去），

∴x=

（3）

解：

因为MN的长度固定，故点P到MN的距离最大时，△PMN的面积最大，

∴可设另一直线y=x+b与y2相交于点P，很显然它们只有一个交点时，满足条件．

即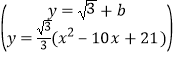：只有唯一一个解的时候，这个点就是点P，

即方程x+b=（x2﹣10x+21）有唯一一个解，

解得：x=，

将x=代入y2=(X2-10X+21)，解得y=,

故点P的坐标为(，)

【解析】（1）对点A、B、C坐标的意义要明白，点A与点B是二次函数与横轴的交点，点C是纵轴的交点，关于x=3意义的理解，就是将y1=（x2﹣2x﹣3）（x≤3）进行了平移，从而可求得抛物线y2的解析式；
（2）要理解，只有当CM垂直平分AD时，才能在y2找到点M，故点M即为直线（C与AD的中点P连线）的交点；
（3）显然MN的值固定，即在y2上的点，到CM的距离最大的点，即与CM平行的直线与y2只有一个交点时，即为所求．
【考点精析】本题主要考查了图形的平移和菱形的性质的相关知识点，需要掌握对应线段,对应点所连线段平行（或在同一直线上）且相等；对应角相等；平移方向和距离是它的两要素；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能正确解答此题．