题目内容
【题目】已知：如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．求证：
（1）△CDE≌△DBF
（2）OA=OD
【答案】
（1）
证明：∵DE、DF是△ABC的中位线，
∴DF=CE，DF∥CE，DB=DC．
∵DF∥CE，
∴∠C=∠BDF．
在△CDE和△DBF中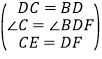
，
∴△CDE≌△DBF （SAS）
（2）
证明：∵DE、DF是△ABC的中位线，
∴DF=AE，DF∥AE，
∴四边形DEAF是平行四边形，
∵EF与AD交于O点，
∴AO=OD
【解析】（1）根据三角形中位线，可得DF与CE的关系，DB与DC的关系，根据SAS，可得答案；
（2）根据三角形的中位线，可得DF与AE的关系，根据平行四边形的判定与性质，可得答案．
练习册系列答案
阅读快车系列答案
相关题目
