题目内容
【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.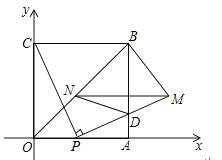
(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小.
【答案】
(1)
解:作ME⊥x轴于E,如图1所示:
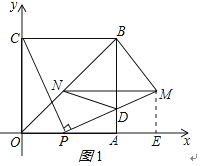
则∠MEP=90°,ME∥AB,
∴∠MPE+∠PME=90°,
∵四边形OABC是正方形,
∴∠POC=90°,OA=OC=AB=BC=4,∠BOA=45°,
∵PM⊥CP,
∴∠CPM=90°,
∴∠MPE+∠CPO=90°,
∴∠PME=∠CPO,
在△MPE和△PCO中,
 ,
,
∴△MPE≌△PCO(AAS),
∴ME=PO=t,EP=OC=4,
∴OE=t+4,
∴点M的坐标为:(t+4,t).
(2)
解:线段MN的长度不发生改变;理由如下:
连接AM,如图2所示:
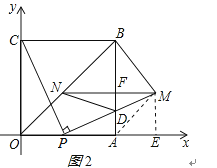
∵MN∥OA,ME∥AB,∠MEA=90°,
∴四边形AEMF是矩形,
又∵EP=OC=OA,
∴AE=PO=t=ME,
∴四边形AEMF是正方形,
∴∠MAE=45°=∠BOA,
∴AM∥OB,
∴四边形OAMN是平行四边形,
∴MN=OA=4;
(3)
解:∵ME∥AB,
∴△PAD∽△PEM,
∴![]() ,
,
即![]() ,
,
∴AD=![]() t2+t,
t2+t,
∴BD=AB﹣AD=4﹣(![]() t2+t)=
t2+t)=![]() t2﹣t+4,
t2﹣t+4,
∵MN∥OA,AB⊥OA,
∴MN⊥AB,
∴四边形BNDM的面积S=![]() MNBD=
MNBD=![]() ×4(
×4(![]() t2﹣t+4)=
t2﹣t+4)=![]() (t﹣2)2+6,
(t﹣2)2+6,
∴S是t的二次函数,
∵![]() >0,
>0,
∴S有最小值,
当t=2时,S的值最小;
∴当t=2时,四边形BNDM的面积最小.
【解析】(1)作ME⊥x轴于E,则∠MEP=90°,先证出∠PME=∠CPO,再证明△MPE≌△PCO,得出ME=PO=t,EP=OC=4,求出OE,即可得出点M的坐标;
(2)连接AM,先证明四边形AEMF是正方形,得出∠MAE=45°=∠BOA,AM∥OB,证出四边形OAMN是平行四边形,即可得出MN=OA=4;
(3)先证明△PAD∽△PEM,得出比例式![]() ,得出AD,求出BD,求出四边形BNDM的面积S是关于t的二次函数,即可得出结果.
,得出AD,求出BD,求出四边形BNDM的面积S是关于t的二次函数,即可得出结果.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案





