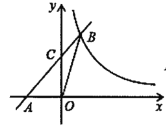
题目内容
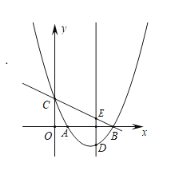
【题目】如图,直线l1:y=![]() x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
(1)求直线l2的解析式,并直接判断△ABC的形状(不需说明理由);
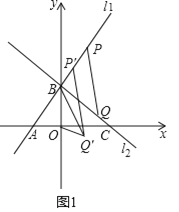
(2)如图1,P为直线l1上一点,横坐标为12,Q为直线l2上一动点,当PQ+![]() CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
【答案】(1)![]() ,△ABC为直角三角形;(2)Q'(
,△ABC为直角三角形;(2)Q'(![]() )
)
【解析】
(1)根据l1求出A,B的坐标,再根据AB:BC=3:4.得出C点坐标,即可求出l2的解析式与△ABC的形状;(2)由题意知当P、Q、M三点共线,且PM⊥x轴时,PQ+![]() CQ最小,利用直线平移的性质与Q点坐标求出l3的解析式,作点B(0,12)关于l3的对称点B',则B'(24,﹣6),连接OB',与直线l3的交点即为所求点Q',再联立l3与直线OB'即可求出Q'的坐标.
CQ最小,利用直线平移的性质与Q点坐标求出l3的解析式,作点B(0,12)关于l3的对称点B',则B'(24,﹣6),连接OB',与直线l3的交点即为所求点Q',再联立l3与直线OB'即可求出Q'的坐标.
解:(1)由l1:y=![]() x+12得B(0,12),A(-9,0)
x+12得B(0,12),A(-9,0)
∴AB=15,
∵AB:BC=3:4.
∴BC=20,故C(16,0)
故求得l2:![]() ,
,
∵AB=15,BC=20,AC= 9+16=25,故AB2+BC2=AC2,
∴△ABC为直角三角形.
(2)当P、Q、M三点共线,且PM⊥x轴时,PQ+![]() CQ最小,
CQ最小,
∴Q(12,3)
平移过程中,点Q'在直线l3上移动,
∵l3∥l1且l3经过点Q(12,3),
∴l3:![]()
作点B(0,12)关于l3的对称点B',则B'(24,﹣6),连接OB',与直线l3的交点即为所求点Q',
∵直线OB':![]() ,
,
∴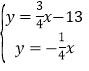 解得
解得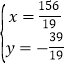 ,
,
∴Q'(![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目