Question

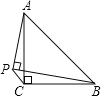
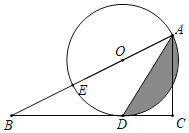
【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，点E在AB上，以AE为直径的⊙O经过点D．

（1）求证：直线BC是⊙O的切线；

（2）若∠B=30°，AC=3，求图中阴影部分的面积．

Answer 1

【答案】（1）证明见解析；（2）π-．

【解析】

（1）连接OD，由AD平分∠BAC，可知∠OAD=∠CAD，易证∠ODA=∠OAD，所以∠ODA=∠CAD，所以OD∥AD，由于∠C=90°，所以∠ODB=90°，从而可证直线BC是⊙O的切线；
（2）根据含30度角的直角三角形性质可求出AB的长度，然后求出∠AOD的度数，然后根据扇形的面积公式即可求出答案．

解：（1）连接OD，

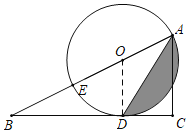
∵AD平分∠BAC，

∴∠OAD=∠CAD，

∵OA=OD，

∴∠ODA=∠OAD，

∴∠ODA=∠CAD，

∴OD∥AD，

∵∠C=90°，

∴∠ODB=90°，

∴OD⊥BC，

∴直线BC是⊙O的切线；

（2）由∠B=30°，∠C=90°，∠ODB=90°，

得：AB=2AC=6，OB=2OD，∠AOD=120°，

∠DAC=30°，

∵OA=OD，

∴OB=2OA，

∴OA=OD=2，

由∠DAC=30°，得DC=，

∴S阴影=S扇形OAD-S△OAD

=π×4-×2×

=π-．