题目内容
已知:如图,抛物线c1经过A,B,C三点,顶点为D,且与x轴的另一个交点为E.
(1)求抛物线c1解析式;
(2)求四边形ABDE的面积;
(3)△AOB与△BDE是否相似,如果相似,请予以证明;如果不相似,请说明理由;
(4)设抛物线c1的对称轴与x轴交于点F,另一条抛物线c2经过点E(抛物线c2与抛物线c1不重合),且顶点为M(a,b),对称轴与x轴相交于点G,且以M,G,E为 顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
(1)求抛物线c1解析式;
(2)求四边形ABDE的面积;
(3)△AOB与△BDE是否相似,如果相似,请予以证明;如果不相似,请说明理由;
(4)设抛物线c1的对称轴与x轴交于点F,另一条抛物线c2经过点E(抛物线c2与抛物线c1不重合),且顶点为M(a,b),对称轴与x轴相交于点G,且以M,G,E为
 顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)(1)设c1的解析式为y=ax2+bx+c,由图象可知:c1过A(-1,0),B(0,3),C(2,3)三点.
解得:
∴抛物线c1的解析式为y=-x2+2x+3.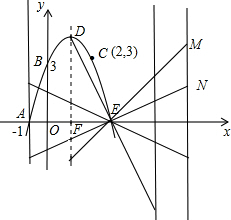
(2)∵y=-x2+2x+3=-(x-1)2+4.
∴抛物线c1的顶点D的坐标为(1,4);
过D作DF⊥x轴于F,由图象可知:OA=1,OB=3,OF=1,DF=4;
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3
∴OE=3,则FE=2.
S△ABO=
OA•OB=
×1×3=
;
S△DFE=
DF•FE=
×4×2=4;
S梯形BOFD=
(BO+DF)•OF=
.
∴S四边形ABDE=S△AOB+S梯形BOFD+S△DFE=9(平方单位).
(3)如图,过B作BK⊥DF于K,则BK=OF=1.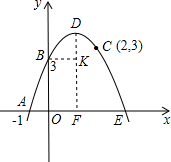
DK=DF-OB=4-3=1.
∴BD=
=
,
又DE=
=2
;
AB=
,BE=3
;
在△ABO和△BDE中,
AO=1,BO=3,AB=
;
BD=
,BE=3
,DE=2
.
∵
=
=
=
∴△AOB∽△DBE.
(4)
,
,
,
,
,
,
.
|
解得:
|
∴抛物线c1的解析式为y=-x2+2x+3.

(2)∵y=-x2+2x+3=-(x-1)2+4.
∴抛物线c1的顶点D的坐标为(1,4);
过D作DF⊥x轴于F,由图象可知:OA=1,OB=3,OF=1,DF=4;
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3
∴OE=3,则FE=2.
S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
S△DFE=
| 1 |
| 2 |
| 1 |
| 2 |
S梯形BOFD=
| 1 |
| 2 |
| 7 |
| 2 |
∴S四边形ABDE=S△AOB+S梯形BOFD+S△DFE=9(平方单位).
(3)如图,过B作BK⊥DF于K,则BK=OF=1.
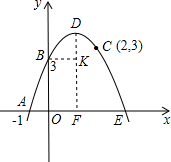
DK=DF-OB=4-3=1.
∴BD=
| DK2+BK2 |
| 2 |
又DE=
| DF2+FE2 |
| 5 |
AB=
| 10 |
| 2 |
在△ABO和△BDE中,
AO=1,BO=3,AB=
| 10 |
BD=
| 2 |
| 2 |
| 5 |
∵
| AO |
| BD |
| BO |
| BE |
| AB |
| DE |
| 1 | ||
|
∴△AOB∽△DBE.
(4)
|
|
|
|
|
|
|

练习册系列答案
相关题目


 BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.