Question

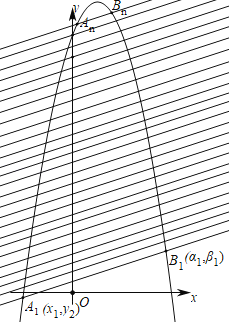
【题目】已知二次函数y＝﹣x2+5x+2019，有一组平行直线与该函数的相交情况如下：

y1＝2x+1与之交于A1（x1，y1）、B1（α1，β1），

y2＝2x+2与之交于A2（x2，y2）、B1（α2，β2），

y3＝2x+3与之交于A1（x3，y3）、B1（α3，β3），

……

yn＝2x+n与之交于An（xn，yn）、Bn（αn，βn），

（1）求x1+α1与x2+α2的值；

（2）求整数n的最大值；

（3）求（x1+x1+x3+…+xn）+（α1+α2+α3+．…+αn）的值．

Answer 1

【答案】（1）x1+α1＝3，x2+α2＝3；（2）2021；（3）3n．

【解析】

（1）将二次函数与一次函数的解析式联立方程，再由一元二次方程的根与系数的关系解答即可；

（2）当y＝2x+n与抛物线y＝﹣x2+5x+2019有一个交点时，此时n最大，利用△＝0即可求解；

（3）先将所求式子转化为（x1+a1）+（x2+α2）+…+（xn+αn），再结合（1）题的结论即可求解．

解：（1）由题意可得2x+1＝﹣x2+5x+2019，即x2－3x－2018=0，

∵x1、α1是上述方程的两个根，∴x1+α1＝3；

同理2x+2＝﹣x2+5x+2019，即x2－3x－2017=0，

∵x2、α2是上述方程的两个根，∴x2+α2＝3；

（2）2x+n＝﹣x2+5x+2019，即x2﹣3x+n﹣2019＝0，

当△＝0时，可得9﹣4n+8076＝0，解得：n＝2021.25，

∵n为整数，∴n的最大值是2021；

（3）由（1）得：x1+α1＝3，x2+α2＝3，…，xn+αn＝3；

∴（x1+x1+x3+…+xn）+（α1+α2+α3+…+αn）＝（x1+a1）+（x2+α2）+…+（xn+αn）＝3n．