题目内容
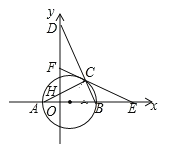
【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)、C(3,2![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
【答案】(1)3;(2)见解析
【解析】
(1)作CG⊥x轴于G,根据勾股定理和射影定理即可得到结论;
(2)连接PC,由AB是⊙P的直径,得到∠ACB=90°根据等腰三角形的性质得到∠PCB=∠PBC,根据切线的判定定理即可得到结论.
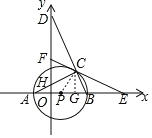
(1)作CG⊥x轴于G,
∴AG=3-(-1)=4,CG=![]() ,
,
则AC2=AG2+CG2=42+(2![]() )2=24,
)2=24,
由射影定理得:AC2=AGAB,
∴AB![]() 6,
6,
∴⊙P的半径为3;
(2)连接PC.
∵AB是⊙P的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°.
∵PC=PB,
∴∠PCB=∠PBC.
∵∠CAB=∠DCF=∠ECB,
∴∠ECB+∠PCB=90°.
∵C在⊙P上,
∴CE是⊙P的切线.

练习册系列答案
相关题目