题目内容
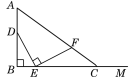
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=![]() DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
【答案】A
【解析】
作FM⊥BC于M.由△DBE≌△EMF,推出FM=BE=x,EM=BD=2BE=2x,由FM∥AB,推出![]() ,即
,即![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
解:作FM⊥BC于M.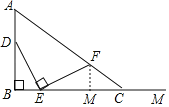
∵∠DBE=∠DEF=∠EMF=90°,
∴∠DEB+∠BDE=90°,∠DEB+∠FEM=90°,
∴∠BDE=∠FEM.
在△DBE和△EMF中,
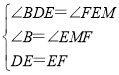
∴△DBE≌△EMF,
∴FM=BE=x,EM=BD=2BE=2x,
∵FM∥AB,
∴![]() ,即
,即![]() =
=![]() ,
,
∴y=-![]()
故选A.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目