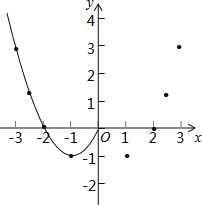题目内容
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④当x<1时,y<0.其中正确的命题是( )
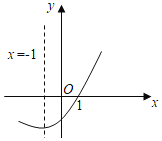
A.②③B.①③C.①②D.①③④
【答案】B
【解析】
利用x=1时,y=0可对①进行判断;利用对称轴方程可对②进行判断;利用对称性确定抛物线与x轴的另一个交点坐标为(-3,0),则根据抛物线与x轴的交点问题可对③进行判断;利用抛物线在x轴下方对应的自变量的范围可对④进行判断.
∵x=1时,y=0,
∴a+b+c=0,所以①正确;
∵抛物线的对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∴b=2a,所以②错误;
∵抛物线与x轴的一个交点坐标为(1,0),
而抛物线的对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点坐标为(﹣3,0),
∴方程ax2+bx+c=0的两根分别为﹣3和1,所以③正确;
当﹣3<x<1时,y<0,所以④错误.
故选:B.

练习册系列答案
相关题目
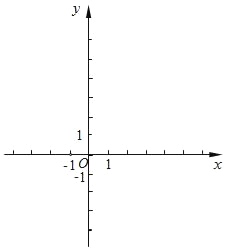
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .