Question

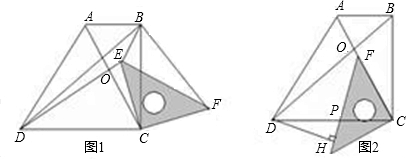
在梯形ABCD中，AB∥CD，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2；对角线相交于O点，等腰直角三角板的直角顶点落在梯形的顶点C上，使三角板绕点C旋转．
（1）当三角板旋转到图1的位置时，猜想DE与BF的数量关系，并加以证明；
（2）在（1）问条件下，若BE：CE=1：2，∠BEC=135°，求sin∠BFE的值；
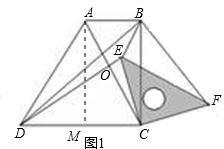
（3）当三角板的一边CF与梯形对角线AC重合时，作DH⊥PE于H，如图2，若OF=

5

6

时，求PE及DH的长．

Answer 1

分析：（1）相等，证DE与BF所在的三角形全等即可；
（2）易得∠BEF=90°，那么可得到△BEF各边的比值进而求解；
（3）根据△CFP∽△CDO，利用相似三角形的性质解答．

解答：解：（1）当三角板旋转到图1的位置时，DE=BF，

∵∠ECB+∠BCF=90°，∠DCE+∠ECB=90°，
∴∠DCE=∠BCF．
∵∠BCD=90°，AB∥CD
∴∠ABC=90°，∠BAC=∠ACD，
∵BC=2，AB=1，
∴tan∠BAC=2，
∵tan∠ADC=2，
∴∠BAC=∠ADC，
∴∠ACD=∠ADC，
∴AD=AC，
作AM⊥CD于点M，
∴CD=2MC=2AB=2，
∴CD=BC．
∵EC=CF，
∴△DCE≌△BCF．
∴DE=BF．

（2）∵∠BEC=135°，∠FEC=45°，
∴∠BEF=90°．
∵BE：CE=1：2，
∴BE：EF=1：2

2

．
∴sin∠BFE=BE：BF=

1

3

．

（3）

∵△CFP∽△CDO，
CF：CD=CP：CO=PF：DO
AC=

5

，
AO：CO=1：2，CO=

2 5

3

，
CF=

2 5

3

-

5

6

=

5

2

，

5

2

：2=CP：

2 5

3

，
CP=

5

6

，
∵DB=2

2

，BO：DO=1：2，
∴DO=

4 2

3

，
∴PF=

10

3

，PE=

2

×

5

2

-

10

3

=

10

6

，
DP=2-

5

6

=

7

6

，
做CN垂直PF于N，
DH：CN=DP：CP，
DH：

5 2

2

=

7

6

：

5

6

，
DH=

7 10

20

．
故PE=

10

6

，DH=

7 10

20

．

点评：两条线段相等，通常是证这两条线段所在的三角形全等；注意使用已得到的结论．