题目内容
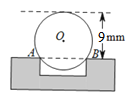
【题目】如图,已知AE、BD相交于点C,AC=AD,BC=BE,F、G、H分别是DC、CE、AB的中点.求证:
(1)HF=HG;
(2)∠FHG=∠DAC.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接AF,BG.根据等腰三角形的三线合一得到直角三角形,再根据直角三角形斜边上的中线等于斜边的一半进行证明;
(2)根据直角三角形斜边上的中线等于斜边的一半得到FH=BH,则∠HFB=∠FBH,同理∠AGH=∠GAH,则∠D=∠ACD=∠CAB+∠ABC=∠BFH+∠AGH.从而证明结论.
证明:(1)连接AF,BG,
∵AC=AD,BC=BE,F、G分别是DC、CE的中点,
∴AF⊥BD,BG⊥AE.
在直角三角形AFB中,
∵H是斜边AB中点,
∴FH=![]() AB.
AB.
同理得HG=![]() AB,
AB,
∴FH=HG.
(2)∵FH=BH,
∴∠HFB=∠FBH;
∵∠AHF是△BHF的外角,
∴∠AHF=∠HFB+∠FBH=2∠BFH;
同理∠AGH=∠GAH,∠BHG=∠AGH+∠GAH=2∠AGH,
∴∠ADB=∠ACD=∠CAB+∠ABC=∠BFH+∠AGH.
又∵∠DAC=180°﹣∠ADB﹣∠ACD,
=180°﹣2∠ADB,
=180°﹣2(∠BFH+∠AGH),
=180°﹣2∠BFH﹣2∠AGH,
=180°﹣∠AHF﹣∠BHG,
而根据平角的定义可得:∠FHG=180°﹣∠AHF﹣∠BHG,
∴∠FHG=∠DAC.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目