��Ŀ����
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����E�ӵ�A��������ÿ��
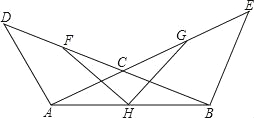
����E�ӵ�A��������ÿ��![]() ����λ���ȵ��ٶ��ر�AC���յ�C�˶���E�������ͬʱ����F�ӵ�B��������ÿ��2����λ���ȵ��ٶ��ر�BA���յ�A�˶�������EF�����߶�EF�Ƶ�F��ʱ����ת
����λ���ȵ��ٶ��ر�AC���յ�C�˶���E�������ͬʱ����F�ӵ�B��������ÿ��2����λ���ȵ��ٶ��ر�BA���յ�A�˶�������EF�����߶�EF�Ƶ�F��ʱ����ת![]() �õ��߶�FG����EF��FGΪ����������EFGH�����F�˶���ʱ��Ϊt��
�õ��߶�FG����EF��FGΪ����������EFGH�����F�˶���ʱ��Ϊt��![]()
![]() �ú�t�Ĵ���ʽ��ʾ��E����AB�ľ��룻
�ú�t�Ĵ���ʽ��ʾ��E����AB�ľ��룻
![]() ����G���ڱ�AB��ʱ����t��ֵ��
����G���ڱ�AB��ʱ����t��ֵ��
![]() ����BG����
����BG����![]() �����ΪS��ƽ����λ
�����ΪS��ƽ����λ![]() ����S��t֮��ĺ�����ϵʽ��
����S��t֮��ĺ�����ϵʽ��
![]() ֱ��д��������EFGH�Ķ���H��G�ֱ����A��C�������ʱ��tֵ��
ֱ��д��������EFGH�Ķ���H��G�ֱ����A��C�������ʱ��tֵ��
���𰸡�![]() ��E����AB�ľ�����t��
��E����AB�ľ�����t��![]() ��
��![]()
![]() ��
��![]() ��
��
��������
(1)�����߶�ED���������Ǻ�����DE�ij������ǵ�E����AB�ľ��룻
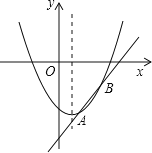
(2)����G���ڱ�AB��ʱ����ͼ2����ʱEF��AB������ͬ�ǵ����Ǻ�����ʽ�����t��ֵ��
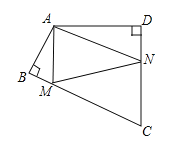
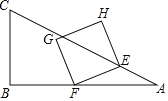
(3)������������ٵ�0��t��1ʱ����ͼ3��������GP�����ݡ�GPF�ա�FDE����GP=DF=4-4t�����������ʽ��S���ɣ��ڵ�1<t��2ʱ����ͼ4��ͬ��������������ۣ�
(4)��E��C�غϣ�F��A�غ�ʱ��AH=CG����t=2��
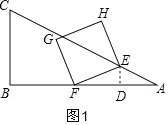
![]() ��ͼ1����E��
��ͼ1����E��![]() ��D��
��D��
.
������ã�![]() ��
��
![]() �У��ɹ��ɶ����ã�
�У��ɹ��ɶ����ã�![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
���E����AB�ľ�����t��
![]() ����G���ڱ�AB��ʱ����ͼ2����ʱ
����G���ڱ�AB��ʱ����ͼ2����ʱ![]() ��
��
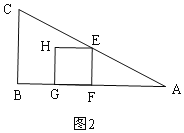
��![]() �ã�
�ã�![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() �����������
�����������
![]() ��
��![]() ʱ����ͼ3����E��
ʱ����ͼ3����E��![]() ��D����G��
��D����G��![]() ��P��
��P��
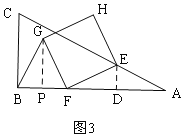
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
��֤![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ʱ����ͼ4����E��
ʱ����ͼ4����E��![]() ��M����G��
��M����G��![]() ��N��
��N��
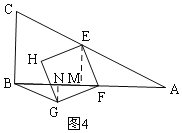
��֤![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����������S��t֮��ĺ�����ϵʽΪ��
![]() ��
��
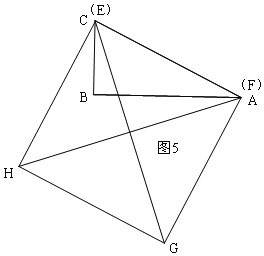
![]() ������EFGH�Ķ���H��G�ֱ����A��C�������ʱ����ͼ5����ʱE��C�غϣ�F��A�غϣ�
������EFGH�Ķ���H��G�ֱ����A��C�������ʱ����ͼ5����ʱE��C�غϣ�F��A�غϣ�
![]() ��
��