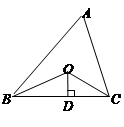题目内容
师在一次“探究性学习”课中,给出如下数表:
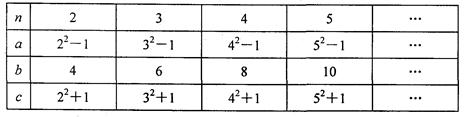
(1)请你分别认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式表示:
a= ,b= ,c= .
(2)猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的理由.

(1)请你分别认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式表示:
a= ,b= ,c= .
(2)猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的理由.
(1)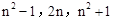 ;(2)以a,b,c为边的三角形是直角三角形,理由见解析.
;(2)以a,b,c为边的三角形是直角三角形,理由见解析.
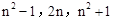 ;(2)以a,b,c为边的三角形是直角三角形,理由见解析.
;(2)以a,b,c为边的三角形是直角三角形,理由见解析.试题分析:(1)结合表中的数据,观察a,b,c与n之间的关系,可直接写出答案;(2)分别求出a2+b2,c2,比较即可.
试题解析:(1)由题意有:
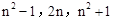 .
.(2)猜想为:以a,b,c为边的三角形是直角三角形.理由如下:
∵
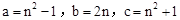 ,
,∴
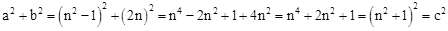 .
.∴根据勾股定理的逆定理可知以a,b,c为边的三角形是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的周长是21,OB,OC分别平分∠ABC和∠ACB,
的周长是21,OB,OC分别平分∠ABC和∠ACB,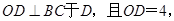 △ABC的面积是_______.
△ABC的面积是_______.