��Ŀ����
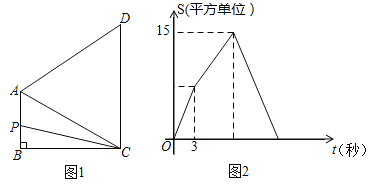
����Ŀ��Ϊ�ƹ�������������μ䡱�������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢���ͳ��ͼ������ͼ�е���Ϣ����������⣺
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
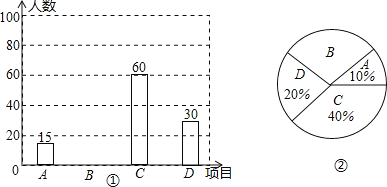
���𰸡���1������������У���������150��ѧ����
��2�����������ϲ����������Զ����ѧ��������45�ˣ���ռ�ٷֱ���30%��ͼ�μ�������
��3���պó鵽ͬ�Ա�ѧ���ĸ�����![]() ��
��
��������
������1����A������������ռ�İٷֱȣ�������������ѧ������
��2���ó�����������ȥA��C��D�����������ϲ����������Զ����ѧ���������ٳ��Ա������ѧ�����������ռ�İٷֱȣ��ٻ�ͼ���ɣ�
��3����A��ʾ������B��ʾŮ������������ͼ���ٸ��ݸ��ʹ�ʽ���м��㼴����
�����������1����������ã�
15��10%=150��������
��������������У���������150��ѧ����
��2�����������ϲ����������Զ����ѧ�������ǣ�150��15��60��30=45���ˣ���
��ռ�ٷֱ��ǣ�![]() ��100%=30%��
��100%=30%��
��ͼ���£�
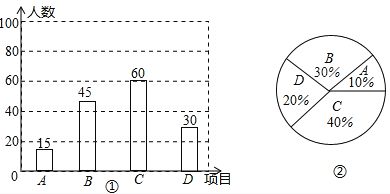
��3����A��ʾ������B��ʾŮ������ͼ���£�

����20�������ͬ�Ա�ѧ���������8�֣�
��պó鵽ͬ�Ա�ѧ���ĸ�����![]() =
=![]() ��
��

 �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�