Question

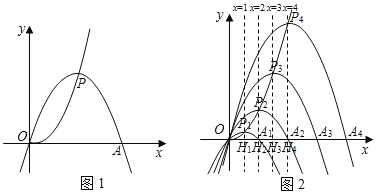
【题目】如图，直线与顶点为的抛物线的交点在轴上，交点在轴上．

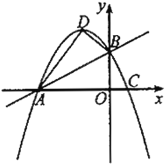
（1）求抛物线的解析式．

（2）是否为直角三角形，请说明理由．

（3）在第二象限的抛物线上，是否存在异于顶点的点，使与的面积相等？若存在，求出符合条件的点坐标．若不存在，请说明理由．

（4）在第三象限的抛物线上求出点，使．

Answer 1

【答案】（1）；（2）不是直角三角形，理由见解析；（3）存在，；（4）点.

【解析】

（1）待定系数法即可求出；

（2）取中点，根据点的坐标关系判断即可证明；

（3）设的解析式为，代入D点坐标可求出，通过解方程，若有解，即可证明存在；

（4）设直线的解析式为并求出，进而可求出直线的解析式，联立BF与抛物线解析式即可求得.

解：（1）如图，

由知，，．

则抛物线．

将代入，得．

∴．

∴抛物线解析式为．

（2）不是直角三角形．理由如下

由（1），，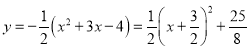

∴顶点．

如图，由（1），可得．

取中点．

则．∴．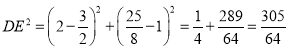

∵，∴不是直角三角形．

（3）如图，存在点，使．

设经过点与平行的直线的解析式为．

将代入，得．∴．

∴的解析式为．

由，整理，得．

解得，．

当时，．

∴．

（4）如图，设直线的解析式为．

则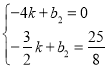解得，．

∴直线的解析式为．

∴经过点与平行的直线的解析式为．

由，整理，得．

解得，或．

当时，．

∴抛物线上点，满足．