题目内容
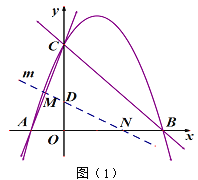
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() .平行于对角线
.平行于对角线![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线![]() 与矩形
与矩形![]() 的两边分别交于点
的两边分别交于点![]() 、
、![]() ,直线
,直线![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
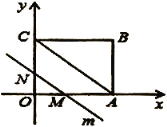
(1)点![]() 的坐标是_______,点
的坐标是_______,点![]() 的坐标是________;
的坐标是________;
(2)在![]() 中,当
中,当![]() 多少秒时,
多少秒时,![]() ;
;
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)(4,0),(0,3);(2)当t=2秒时,![]() ;(3)
;(3)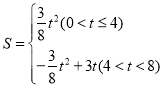 .
.
【解析】
(1)根据BC∥x轴,AB∥y轴即可求得A和C的坐标;
(2)判断出MN是△OAC的中位线进行讨论;
(3)求得AC的函数解析式,E的坐标是(t,0),则直线MN的解析式即可求得,则M和N的坐标即可求得,然后根据“S=矩形OABC的面积﹣Rt△OAM的面积﹣Rt△MBN的面积﹣Rt△NCO的面积”即可求得.
(1)A的坐标是(4,0),C的坐标是(0,3);
(2)∵MN∥AC,且![]() ,
,
∴MN是△OAC的中位线,
∵M是OA的中点,则![]() ;
;
(3)①当0<t≤4时,OM=t,
∵MN∥AC,
∴△OMN∽△OAC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
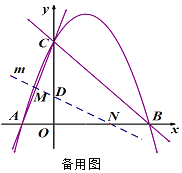
②当4<t<8时,如图,
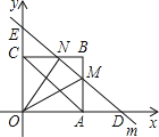
∵OD=t,
∴AD=t﹣4,
∵直线m∥AC,
∴∠MDA=∠CAO,
∴Rt△DAM∽Rt△AOC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理得:△BMN∽△BAC,
∴![]() ,即
,即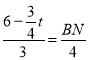 ,
,
∴![]() ,
,
∴CN=4-BN=t﹣4,
S=矩形OABC的面积﹣Rt△OAM的面积﹣Rt△MBN的面积﹣Rt△NCO的面积
![]() ;
;
∴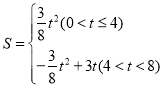 .
.

练习册系列答案
相关题目