题目内容
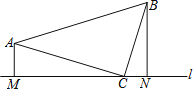
【题目】如图所示，已知四边形ABCD是平行四边形，∠C=70°，若AF、BE分别为∠DAB、∠CBA的平分线．
求证：（1）DF＝EC；（2）求∠DFA的大小。
【答案】(1)见解析;(2)35°.
【解析】
(1)由角平分线的定义得出∠DAF=∠BAF，再由AB∥CD，得∠DFA=∠BAF，从而得出∠DAF=∠DFA，即AD=DF，同理得出BC=EC，由平行四边形的性质得出DF=EC;
(2)先根据平行四边形的性质得出∠DAB=70°,AB∥DC，利用平行线的性质得出∠FAB=∠DFA，再由角平分线得出∠DFA=∠FAB=
∠DAB=35°.
证明：（1）∵AF、BE分别为∠DAB、∠CBA的平分线，
∴∠DAF=∠BAF，
又在四边形ABCD中DC∥AB，
∴∠DFA=∠BAF，
从而，∠DAF=∠DFA
∴AD=DF，同理BC=EC。
又AD=BC
∴DF＝EC
(2)∵四边形ABCD是平行四边形, ∠C=70°, ∴∠DAB=70°,AB∥DC, ∴∠FAB=∠DFA, ∵AF平分∠DAB，∴∠FAB=∠DAB=35°, ∴∠DFA=∠DAF=35°.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，完成下列题目：
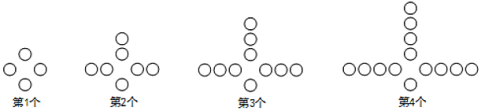
（1）填写下表：
图案序号 | 1 | 2 | 3 | 4 | … |
|
○个数 | 4 | 7 | … |
（2）若按上面的规律继续摆放，是否存在第
个图形，其中恰好含有2020个○?
