题目内容
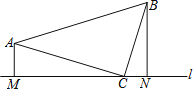
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由垂直定义得∠AMC =∠BNC=90°,再根据同角的余角相等得∠MAC=∠NCB,再由AAS证明△AMC≌△CNB.
(2)由△AMC≌△CNB得出CM=BN=5,再利用勾股定理就能计算BC,从而算出AB.
解:(1)∵AM⊥l,BN⊥l,∠ACB=90°,
∴∠AMC=∠ACB=∠BNC=90°,
∴∠MAC+∠MCA=90°,∠MCA+∠NCB=180﹣90°=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
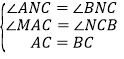
∴△AMC≌△CNB(AAS);
(2)由(1)知 △AMC≌△CNB,
∴CM=BN=5,
∴Rt△ACM中,AC=![]() ,
,
∵Rt△ABC,∠ACB=90°,AC=BC=![]() ,
,
∴AB=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目